Convolved out

Bit of a dry post coming up, but when you consider I blew my Sunday on this it might make sense. Curiosity got the better of me today and I spent most of it playing with convolutions with OpenCL on a GPU - I had a pretty fast implementation but wanted to compare it with some other ideas I had.

As it turned out, the implementation I had was the fastest after-all, although I tweaked it a tiny bit during the process.

For kernels at 3x3 (or 7x7 for 4-channel UBYTE images), a simple 2d implementation is very slightly faster than a more complex algorithm.

For non-separable convolution, a complex implementation which uses a rolling buffer is over 3x faster than a naive implementation, at least up to sizes of 31x31.

For separable convolution, my complex implementation is up to 2.5x faster than a naive implementation.

My separable convolution implementation reads 16x16 blocks of image into local memory and then each thread generates all results from the local memory in one pass - e.g. for up to 7x7 convolution it reads 2x16x16 blocks, for up to 15x15 convolution it reads 3x16x16 blocks, and so on i.e. you need the 16x16 data plus 'kernel radius' pixels each size. It uses transpose for the Y convolution case during load and saving of the data but the processing is identical. It also uses the trick of offsetting the odd rows of the data so they avoid local memory contention when they might otherwise - e.g. when the number of bocks being read is even.

FWIW for 640x480 image on a GTX 480 A single channel FLOAT 31x31 separable convolution is about 190uS, or 470uS for naive version. For UBYTE 177uS vs 470uS. For a 4 channel image the timings are 413uS, 916uS, 389uS, and 465uS respectively. So larger (byte size) images gain more - presumably from the reduction in memory reads and lower cache loading.

Actually - yesterday I started working on a JOCL based image processing library that I intend to drop on google code at some point - and this investigation was part of that. More should be forthcoming on that soon although right now I just don't have enough put together to be much use.

Luser error

So it turns out the main problem with the performance issues in my last post wasn't the cache being overloaded after all ... but the compiler running out of registers to unroll a couple of nested loops I asked it to.

It turns out because of a cut and paste job I left in some test code which was limiting the register count for the compiler, and the register spillage was a bit of a disaster and causing the order of magnitude drop. With this fixed things look a lot more promising, although at ~4ms it is still a little slower than I would like and I can't see much being able to be done to improve it.

It's a bit weird that an unconstrained compile for a specific device would choose to use all registers it needs for the code-unrolling, ignoring the device specifics, but I guess this is some particular of the nvidia opencl implementation.

There is still some problems with the texture cache being hit too hard anyway - the integral image has to be stored using the UINT32 data type, and it needs at least 8 lookups per feature tested which is a pretty heavy load to start with. With the other feature tester I could just use 8 bit images which fits better into the cache it seems (contrary to what i'd believed until this point).

Investigations ongoing ...

Cache only works when there's enough

Update: Seems I was (mostly) wrong - see the follow-up post.

I've been playing with object classifiers in OpenCL - I have one that works, not terribly well but relatively quickly. It's a random tree classifier and just uses pixel intensity comparisons for feature tests. Although I can get some results out of it they just weren't reliable enough.

So I decided to use 2-bit-binary patterns instead, a haar-like feature measure which uses an integral image to accelerate the intensity comparisons (maybe more on the integral image creation another time, that was a bit of a journey in OpenCL as well). Unfortunately the simple modifications required to change the feature detector suddenly blew out the computation time - from under 1ms to over 20ms, making it far too slow. This even though it only requires twice the memory accesses for the same number of tests.

After much experimentation I found the cause - the texture cache was being exhausted, dramatically reducing the apparent memory throughput. I discovered that a single-tree, 3-feature tester is about the limit of the texture cache. That will execute in 150uS. 4-features take 250uS, and if I change the 4-feature system to 2 trees, or 8 features - just twice the amount of work - it blows out to 1500uS.

Well, at least that gives me options for splitting the work into multiple passes and maybe i'll end up with something fast enough over-all. Otherwise I might have to find something else. As it is i'm losing confidence that it is going to be good enough anyway (maybe after running it so many times i've forgotten how poor the previous one was).

Hot Sauce #2 - Sweet Arson

As it turns out it was a rainy day and I thought the fresh habaneros either needed to be used or frozen so I made another sauce today as well.

The week previously I had excavated a patch of sweet potatoes and ended up with a reasonable haul (the largest in the photo is 2.4kg) ... and I had the idea of using the sweet potato as the base for this sauce. And this time I thought i'd try a warming mix of herbs to compliment it. I'm really quite pleased with this one - it has quite an interesting and pleasant flavour and will leave your lips burning from even quite a small amount.

Ingredients

450g	Roasted sweet potato (2-3 average tubers).
12	Cayesan Chillies, roasted.
12	Habaneros, roasted.
150ml	Grapeseed oil.
1	Diced onion.
	Dry Spices
2 tsp	Coriander seed.
1 tsp	Cardomon seed.
1 tsp	Black peppercorns.
1 tsp	Whole allspice.
2	Cloves.
1 tsp	Fennel seed.
	Liquids
2 cups	Malt vinegar.
1 1/2 cup	Water.
1 tsp	Citric Acid.
1 tsp	Salt
1 tsp	MSG

Method

Place the sweet potato whole and un-peeled into a roasting tray and roast until done - about an hour. Place the chillies on another tray and roast until they start to collapse - about 20 minutes. Remove the potatoes from the oven and let them cool to a suitable temperature for handling and peel the skins off (perhaps sweating them under foil will help).

Meanwhile, place the oil and onion in a medium sized saucepan and cook slowly on low heat - so they become translucent but do not brown.

Take the dry seeds and toast lightly in a dry pan for a few minutes. Use a medium heat and constantly move them so they do not burn. Transfer the seeds to a mortar and pestle and pound to a fine dust.

Add the dry spices to the onions and cook for a couple of minutes.

Add the roasted chillies and sweet potato and mash them together.

Add all of the liquid before it starts to burn, together with the remaining ingredients and simmer for at least 30 minutes on a very low heat.

Use a stick blender to thoroughly blend everything into as fine a liquid as it's capable of (i'm using a Tiffany hand-me-down and it struggles but works).

Bottle.

Results

This tastes really nice so far. Very subtle, slightly sweet and nutty flavour with a lip-burning kick to follow up which seems to multiply with every subsequent taste.

I didn't think it was going to end up hot enough after adding the liquid I needed to make it thin enough, so I threw in another half-dozen chopped habaneros when it was nearly done, cooked them for a while and re-blended. This might be the last hot sauce I make for a while too, so I wanted to make sure it counted!

I'd probably rate this 7.5 out of 10 for heat. Update So 6 months on, this is definitely my favourite sauce. I think it could use a bit more heat but the flavour goes with lots of things - i sometimes use it instead of butter on sandwiches, for dipping chips (it gets hot!), or to add a pleasant kick to pasta, steak, or a snag. Please comment if you give it a go ...

Hot Sauce #1 - Toxic Lime

Back with another sauce - this time I thought i'd try something of a Thai theme: lime, kaffier lime, lemongrass, and fresh coriander. I just grabbed a few things from the garden and the pantry that seemed to match and came up with my second sauce, Sauce #1 - Toxic Lime.

Ingredients

350g	Apples, cored.
60g	Fresh coriander, including root and stem.
70g	Fresh lemongrass.
40g	Fresh ginger.
12g	Fresh lemon basil leaves.
2	Kaffir lime leaf.
1	Kaffir lime zest.
2	Limes, juice and zest.
200g	Cayesan chillies (large fleshy chillies)
100g	Habaneros (about 15)
1/2 cup	Malt vinegar.
30g	Palm sugar.
1/2 cup	Cane Sugar.
1 cup	Water.
1 tsp	Citric Acid.
2 tbl	Mushroom soy sauce (Happy Boy Brand)
100ml	Olive oil.

Method

Cut the ginger, lemongrass and lime leaf into fine slices and then put into a food processor and process until finely chopped. Add all of the other fresh ingredients (everything until and including the chillies) and blend thoroughly into a fine paste.

Place into a medium sized saucepan on a low heat and add the liquids and bring to a slow simmer.

Stir in the sugar and simmer everything slowly 'until done' - 30+ minutes.

Use a stick blender to liquefy everything together as much as possible.

Bottle.

Results

This has a slightly strange flavour - despite lime and chilli seeming a good match I've never really found something where it truly 'worked'. Perhaps the kaffier lime zest is a little overpowering, as is the coriander. I will have to leave it for a bit and try it with some suitable food (might go well with pork?).

It definitely has a lime flavour to it though, which is what I was trying to achieve so at this point i'd call it a success. And it smells wonderful. It's probably about a 7 out of 10 for heat as with the previous recipe.

Simple padding trick

For a few algorithms I have, I end up with data which is 32 elements wide operated on by 16x16 threads. This ends up with 100% local memory contention if mapped directly to the local memory since every 16th thread aliases to the same bank.

Although this can be addressed with a 16 word padding this is wasteful of precious local memory which might mean the code can't run in parallel to the extent it might otherwise, or simply cannot fit.

A simple trick which still keeps the addressing quite simple is to shift every odd line to the second half of the data which is then offset by 16 words. In effect bit 0 of the y address is shifted to the top of the addressing index, with an offset.

For example, if a kernel is working on a 16x16 region of memory but requires some data either side of the target tile, it might do something like:

   local float ldata[32*16];
   int lx = get_local_id(0);
   int ly = get_local_id(1);

   int i = lx + ly * 32;

   // load data
   ldata[i] = ..read data block 8 to the left ...;
   ldata[i+16] = ..read data 8 to the right...;
   barrier(CLK_LOCAL_MEM_FENCE);

   // work using i+8 as the centre pixel for this thread

By only changing the calculation of i and padding the storage with only 16 words, the contention is easily removed without changing any other code:

   local float ldata[32*16+16];
   ...

   int i = lx + ( ly >> 1 ) * 32 + (32*8+16)*(y & 1);

   ...

Assuming one is only working in the X direction, for Y the addressing is slightly more complex of course. But this could come at no extra run-time cost once the loops are unwound.

Transpose Is Your Friend

With graphics programming a lot of algorithms can be split into separate X and Y passes. This generally works particularly well in the X case but in Y you can hit issues with memory (or processor) locality which can have a big impact on the algorithm.

But the GPU texture cache is block oriented rather than line oriented so both X and Y oriented algorithms can be implemented equally (in)efficiently if you store data in images. However, once in local memory you're effectively back to line-oriented access ... (if you want to preserve your sanity whilst working out the memory addressing to efficiently access the banked memory).

The trick is just to transpose the data on read and write, and always work in the X direction locally. It also means the X and Y working code is often identical. This can be done just within the local work-group, but for 2D workgroups one has the added complication that work units are allocated in row-major order, i.e. in X first.

The simple solution is just to transpose the global X and Y work-size as well, and simply swap the result of get_global_id(0) and get_global_id(1) when reading or writing the images.

Parallel Prefix Sum

14/9/11: added a further paragraph on additional thoughts

Since coming across the parallel prefix sum a couple of weeks ago, a lot of things I need to solve seem to fall into the class of problems it is suited for within OpenCL on GPU platforms. However after a lot of trial and error and experimentation i've found it is usually just slower - sometimes by quite a margin.

In short, it takes advantage of the very high speed local memory ('LS') and parallelism to compute a commutative result from every element to every previous element in log2(n/2) steps.

But with GPU's there are a couple of problems with it:

1. Even in the ideal case many of the threads are computing redundant data or not operating (depending how one chooses to implement it).
2. A synchronisation step is required after every single operation - which is usually something trivially simple.

The first leads to an over-commitment of threading resources which impacts the scalability as the overall job size increases. And the second leads to very inefficient scheduling even on simple tasks, and a much heavier 'inner loop'.

For example, I implemented a 5x5 maximum operation (for non-maximum suppression peak detection) using a separate X and Y operation (I realise a 5-tap test doesn't really exercise the log2(N) nature of the algorithm much, but more on that later).

My first implementation uses a 16x16 workgroup size (after much experimentation this seems to be the generally best workgroup size for operating on images on my hardware - it leads to an occupancy of 1 and seems to be a good fit for the texture cache configuration). Each local workgroup reads a 16x16 area into LS and then 16 threads work together on each row of result. It only does a couple of 'prefix sum' steps because I only need the result from 4 samples, and I do the last one manually. I use the trick of offsetting the starting point so no thread requires any conditional execution. Finally, it only produces 12 valid results for the 16 inputs since you need overlap.

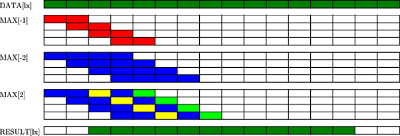
Figure 1: Steps taken for parallel maximum calculation. Only the workings of 4 of the 16 threads are shown.

Because it only generates 12 results it needs to be run 16/12 times the width of the image. This runs in about 65uS on the test data set.

Then I tried a version which reads 2x 16x16 blocks into memory so it can produce all 16 results in one go - unfortunately i've lost the timings and I can't be bothered to re-run it, but i'm fairly confident it wasn't terribly impressive.

Finally I implemented a very simple version which just reads in 2 16x16 blocks into local memory, and then does the operation on the 2 pixels before and 2 pixels after the current location (i.e. an unrolled loop). This was somewhat quicker - 48uS, or about 25% faster.

I didn't bother trying it for the parallel sum case, but I also tried larger window sizes for the simple version - and even at 9 it is still 20% faster than the 5X case for the parallel sum version. And this is for the single channel case - for a 4 channel image you have a 4x LS load, which is not required when it is calculated in registers.

Intuition would tell you that increasing the data-size will eventually lead to a case where it out-performs the simple cases. But the wider the data being calculated the more threads you require and this reduces the opportunity for hiding latencies by letting the GPU schedule independent workgroups. The local store can also be a factor since it too can limit how wide you can go.

I also applied it to (larger) problems where you're only interested in the final result. Because branching is expensive it seems on paper that it doesn't matter if you generate many redundant results since the overall number of steps is much lower - e.g. a 16x16 summation only takes 7 steps rather than 256. Although in reality you break it up into 16 strips 1xwide so it's only 32 steps (16 lots of 16 plus 1 of 16). And it only takes 16 threads rather than 256, so you can execute 16x as many at once for a given number of threads. And you don't need any local store.

I found in all cases it was (sometimes much) faster to split it into 16x1 loops which operate on 16 data items, and then have a single thread complete the partial sums.

And finally the one case where it seemed to have traction - calculating an integral image where every pixel has it's value added to every pixel to the right/below it - did seem faster than another implementation I had. But that initial implementation was before I had discovered other performance improvements so I suspect I could probably do better if i had another go. To satisfy my curiosity I just tried implementing part of it using a looping implementation and with little effort managed to beat or at least equal the prefix-sum version. Incidentally both require splitting the problem into smaller parts and then a final step to 'fix' the integral image - for the parallel prefix sum version you run out of local store or threads, and in both cases you need the parallelism to help improve the GPU efficiency.

Further Thoughts 14/9/11

Since writing this a lot more water has flowed under the bridge and I have a few more thoughts to add.

Having a smaller rather than larger work-size is important as I alluded to above: but larger problems can be made smaller by storing intermediate values in registers and then only sharing the work to reduce a smaller-multiple of the dataset. e.g. storing 4 registers locally allows 4x as much data to be 'processed' using the same amount of shared-work (and shared memory too) - which is the expensive stuff.

Since I was sticking to spec I have never tried removing the barriers and relying on the hardware's behaviour. So I don't know how much difference this makes: the technique in the paragraph above is even more useful then, if you can reduce the problem to the 64 elements required to benefit from the hardware characteristics.

The Integral Image code in socles uses these techniques, and in this case the parallel prefix sum was a (small) win. And IMHO is a fairly tight bit of code.