Wavelet Denoise & Sharpen

So I had some luck with a bit of fiddling with the scaling function for wavelet sharpening. And managed to get both sharpening and smoothing working at the same time. I'm fairly happy with the results.Update: see also a further post on using the DCT in a similar way.Update: I've now implemented a version of this in ImageZ, see the follow-on post

Ok, first the raw Lenna input image I used - converted to greyscale by Java2D. Just to make comparison easier and to add another pretty face to the page.

Now, with the sharpening ramped right up. As you can see it's pretty much the same as using unsharp-mask with a well-selected radius and a medium weight. And like unsharp mask it tends to emphasise any noise.

Unsharp mask/Wiener Deconvolution can still work better if the image is simply de-focussed as they have a PSF function to estimate the amount of defocusing.

Now, with the same settings, and also de-noised very heavily. Despite the obvious and unnatural looking heavy processing the edge sharpness and most of the detail is still retained rather well. Most added artefacts are relatively smooth and natural looking too. If you've ever tried using a median filter or a selective Gaussian blur, you'd know they pretty much suck at retaining any texture detail or clean edges.

And finally, a more natural level of sharpening and de-noising.

Pretty happy with it given how simple the maths is. I've over-emphasised some of the results by using high values, but a smooth variation in results between the original and any of the extreme values is possible.

Two steps are applied to each complex coefficient in turn in a way that can be done whilst the coefficients are in registers. So if you have other processing going on it's essentially free.

Threshold De-noise

C = C * { abs(C) > T ? ( abs(C) - T ) / abs(C) : 0 }

Where:

C the complex transform coefficient;abs(x) returns the magnitude of the complex number x;T input threshold from about 0.01 to 0.001.

(see the previous post for a dead link to the source of this)

This zeros out small coefficients - which are apparently likely to be noise - and scales the rest to their original range.

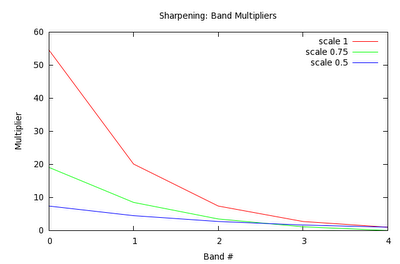
Scale Bands

C = C * { ( exp( (bandcount - nband) * scale) - 1 ) * weight + 1 }

Where:

bandcount is depth of wavelet transform;nband is number of the band (0 is the highest frequency);scale input sharpness 'gradient' from 0-1; andweight input sharpness weight from 0-1.scale is a general 'sharpening factor' setting, and weight specifies how heavily it is applied.

Wavelet Denoise

As a test routine for some low-level code I threw together a little test harness of a complex wavelet de-noise algorithm.It was based on some papers and demo code from this link (which appears to be dead now ... and has been for some time at that). It's just using a very simple threshold-and-scale of the wavelet coefficients, so apart from the relatively expensive Dual-Tree Complex Wavelet Transform it is simple and cheap to implement. The 1.7ms reported is the time to forward transform, apply the thresholding, the inverse, and download the (float) image to Java and convert it to a greyscale byte image. (I know, the screenshot should have been a png, so it's not entirely clear here ...)

This has nothing to do with what i'm working on but I thought it looked quite interesting. It preserves edge detail much better than techniques like a median filter or a Gaussian blur, and introduces fewer artefacts compared to the adaptive blurs i've seen. According to that now-broken-link, using the complex waveform produces subjectively better results compared to the DWT.

Perhaps i could use it as a processing step: if you already have the DTCWT coefficients it's a cheap additional process. Somewhat like doing a convolution in the frequency domain, it's basically free if you're already there.

I also played a bit with working out a sharpening algorithm on the weekend - I couldn't really find any simple papers: they all relied on adaptive processes, and the results reported didn't seems worth all the effort. In the end all I did was linearly scaled the coefficients by some made up numbers. Scale up for the highest frequency components and scale each subsequent wavelet band by 1/2 of the one above.

Unsharp Mask vs Wavelet Sharpen by scaling coefficients with approximately (but not a very good approximation) similar adjustment. Unsharp Mask is on the left.

The result is pretty much the same as unsharp-mask, but it only takes 1 tuning parameter instead of 2, and subjectively it appears to me to a smidgen less noisy. But I need to experiment a bit more, one would expect to be able to reduce the noise compared to unsharp mask and I think my low frequency scaling factors are out and it's affecting the tonal quality too much.

Sharpening ImageZ

I thought it about time to fix a few little bits and pieces with ImageZ that I actually use ... so I tackled some of that. I fixed some of the wiener deconvolution code - so that odd-sized images work for instance. I also tried thoroughly thread-ising it, although I only got a modest performance boost: jtransforms is already using multiple threads for the FFT which is the expensive bit.

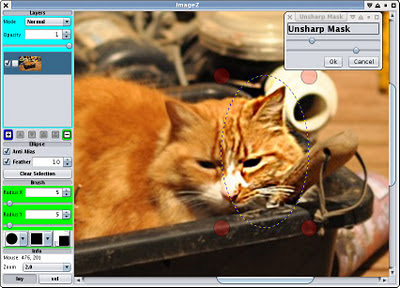
Unsharp mask in a feathered mask. I dialed it up to make it obvious.

Unsharp mask is something I always find really handy, so I finally coded that up too. Rather than start with the mess of the Gaussian filter code I already I have i coded another one from scratch. A bit simpler so I will merge and share the code at some point, or at least put it in a common place. It also mirrors the edges rather than clamping, which seems to produce a more natural response on the edges.

There are still a couple of things I use the gimp for that i'd rather not have to, but I guess that can wait for another day.

I really need to get out of the house this weekend, but i've pretty much pulled up all the weeds, it's been raining enough to water the garden, and the neighbours were using a chainsaw this morning. So I just found myself stuck at the computer again ... and I might watch the rugby on soon too.

Java v OpenCL/CPU

I've been using the AMD CPU driver a bit for debugging and testing: i never really considered it for performance but for various reasons late tonight I ended up poking around with a simple routine and wondered how it compared.

At first I thought i'd discovered a disaster, but that's because I wasn't initialising the data: too many non-normal floating point operations slowing it down significantly. Oops, glad I checked that before posting. Although it's getting late so who knows what else I may have stuffed up.

I was testing using a simple matrix multiply, a 4096x4096 matrix stored in row-major order, multiplied by a 4096 row column-vector. It isn't something i'm in any need of, but after poking around this site which i've read a few times, and with nothing on TV I decided to play around a bit. Then after exhausting my interest on the GPU I tried the CPU version - I was originally going to see if just doing it locally with the CPU driver would be quicker than a device copy and back, but it isn't, the GPU is still 5-10x faster.

I tested 4 implementations:

1. OpenCL written for a CPU target using float types, one work-group and one work-item per row, 4096 work groups
2. OpenCL using float4 types, same
3. Java, single threaded
4. Java, using a ThreadPoolExecutor w/ 12 threads, 32 jobs.

 Code             Time (s)
  Java single      1.5
  Java pool        0.39
  OpenCL float     0.43
  OpenCL float4    0.37

So I had to resort to float4 types to beat the thread pool code, and then only just. It's kind of debatable as to which is easier to write: the Java code must explicitly deal with the range allocation and job launching. But then it's all built-in, and doesn't require a different language, runtime, interface and foreign memory management ... and one that's prone to crashing with zero information, and otherwise and also excruciatingly difficult to debug at that. Ok scratch that: the Java clearly wins here.

One can either conclude that the AMD compiler is a bit below-par to start with (mostly likely true), and only by using vectorised code that it was able to beat the Java. Or perhaps that the hotspot compiler is rather good at this particular problem (again, most likely true), and is possibly using SSE opcodes to implement the loop too. Not that SSEn really seems to add much of a boost in general apart from a few extra registers - it's not like on an SPU where vectorised code can be 10x faster than scalar.

I had until this point thought of the CPU drivers for OpenCL providing a sort of 'portable assembly language' for higher level languages, but if you have a decent compiler already it doesn't seem worth it - at least for some problems.

I suppose another implementation might do better; but you're still stuck with a pretty hostile debugging environment and if you're after performance you'll be using a GPU anyway. So about all it seems useful for is debugging/verifying code. Given that, perhaps it would be useful to add more checking in the compiled code to help with debugging rather than worrying about performance ... Unlike C, OpenCL has a much simpler memory model for which accurate and full run-time address-range-checking can be ?easily? added.

Images vs Arrays 4

Update 7/10/11: I uploaded the array convolution generator to socles

And so it goes ...

I've got a fairly convoluted convolution algorithm for performing a complex wavelet transform and I was looking to re-do it. Part of that re-doing is to move to using arrays rather than image types.

I got a bit side-tracked whilst revisiting convolutions again ... I started with the generator from socles for separable convolution and modified it to work with arrays too. Then I tried a couple of ideas and timed a whole bunch of runs.

One idea I wanted to try was using a rolling buffer to reduce the memory load for the Y convolution. I also wanted to see if using more work-items in a local workgroup to simplify the local memory load would help or hinder. Otherwise it was pretty much just getting an array implementation working. As is often the case I haven't fully tested these actually work, but i'm reasonably confident they should as i fixed a few bugs along the way.

The candidates

convolvex_a

This is a simple implementation which uses local memory and a work-group size of 64x4. 128x4 words of data are loaded into the local memory, and then 64x4 results are generated in parallel purely from the local memory.

convolvey_a

This uses no local memory, and just steps through the addresses vertically, producing 64x4 results concurrently. As all memory loads are coalesced it runs quite well.

convolvex_b

This version tries to use extra work-items just to load the memory, after wards only using 64x4 threads. In some testing I had for small jobs this seemed to be a win, but for larger jobs it is a big hit to concurrency.

convolvey_b

This version uses a 64x4 `rolling buffer' to cache image values for all items in the work-group. For each row of the convolution, the data is loaded once rather than 4x.

imagex, imagey

Is from the socles implementation in ConvolveXYGenerator which uses local memory to cache input data.

simplex, simpley

Is from the socles implementation in ConvolveXYGenerator which relies on the texture cache only.

convolvex_a(limit)

Is a version of convolvex_a which attempts to only load the amount of memory it needs, rather than doing a full work-group width each time.

convolvex_a(vec)

Is a version of convolvex_a which uses simple vector types for the local cache, rather than flattening all access to 32-bits to avoid bank conflicts. It is particularly poor with 4-channel input.

The array code implements CLAMP_TO_EDGE for source reads. The image code uses a 16x16 worksize, the array code 64x4. The image data is FLOAT format, and 1, 2, or 4 channels wide. The array data is float, float2, or float4. Images and arrays represent a 512x512 image. GPU is Nvidia GTX 480.

Results

The timing results - all timings are in micro-seconds as taken from computeprof. Most were invoked for 1, 2, or 4 channels and a batch size of 1 or 4. Image batches are implemented by multiple invocations.

                        batch=1                 batch= 4
channels                1       2       4       1       2       4

convolvex_a             42      58      103     151     219     398
convolvey_a             59      70      110     227     270     429

convolvex_b             48      70      121     182     271     475
convolvey_b             85      118     188     327     460     738

imagex                  61      77      110     239     303     433
imagey                  60      75      102     240     301     407

simplex                 87      88      169
simpley                 87      87      169

convolvex_a (limit)     44      60      95      160     220     366
convolvex_a (vec)               58      141

Thoughts

• The rolling cache for the y convolution is a big loss. The address arithmetic and need for synchronisation seems to kill performance. So much for that idea. I guess there just isn't enough work to do each loop to make it work it (it only requires a single mad per thread).
• Using more threads for loading, then dropping back when doing arithmetic is also a loss for larger problems since it limits how many groups of workgroups can execute on an SM.
• Trying to reduce the memory accesses to only those required slows things down until you hit 4 element vectors. I guess for float and float2 the cached reads are effectively free, whereas the divergent branch is not.
• Even with the texture cache, images benefit significantly from using a local cache.
• Even with the local cache, images trail the array implementation - until one processes 4-element vectors, in which case they are even stevens for single images.
• Arrays can also be batched - processing 'n' separate images concurrently. This adds a slight extra benefit as it can more fully utilise the SM cores, and reduces the need for extra host interaction. For smaller problems this could be important although this problem size is already giving the GPU a good sized workout so the differences are minimal.
• Using single-channel data is under-utilising the GPU by quite a bit.

When I get time and work out how i want to do it i'll drop the array code into socles.

Images vs Arrays 3

So i've been working on some code that works with lots of 2d array data: which gives me the option of using arrays or images.

And ... arrays won out: for simple memory access and writing they are somewhat faster than using images. And that's before you add the ability to batch-process: with images you're pretty much stuck with having to pass each one at a time and only pack up to 4 values in each element (3D image writes are not supported on my platform atm). With arrays you can process multiple 2D levels at once, or even flatten them if they are element-by-element - which can allow you to better fit the problem to the available CUs.

In some cases the improvements were dramatic where a lot of writes to different arrays were required (but the writes were otherwise independent).

Anyway, one particular area I thought images would still be a noticeable win is with some interpolation code I had to implement. I need to do fixed power of 2 scaling up and down. Apart from the bi-linear interpolation 'for free', there is also an interesting note in graphics gems 2 about using the bi-linear interpolation of the texture unit to perform bi-cubic interpolation using only 4 texture fetches rather than 16.

So I ran some tests with both an image and array implementation of the following algorithms:

1. Bi-linear interopolation.
2. Fast Bi-cubic using the graphics gems algorithm with a 64-element lookup table (I found the lookup-table version significantly faster than the calculated one).
3. Bi-cubic using 64-element lookup tables generated from the convolution algorithm in wikipedia.

In both cases I was using float data, a 512x512 image, and 4x scaling in X and Y, and the numbers are in uS from the Nvidia profiler. The array implementation is doing CLAMP_TO_EDGE.

The results were quite interesting.

                        Image           Array
bi-linear               40              36
fast bi-cubic           56              79
table bi-cubic          106             63

With this sort of regular access, the array version of the bi-linear interpolation is actually slightly faster than the image version, although they approach each other as the scale approaches 1. This is a bit surprising.

Images do win out for bi-cubic interpolation, but the array version isn't too far off.

And in either case, the bi-cubic interpolation is really fairly cheap: only about 1.5x the cost of bi-linear which is 'pretty cool' considering how much more work is being done.

I also started to investigate a bi-cubic interpolator that uses local memory to cache the region being processed by the local work-group. Since the actual memory lookups are very regular and the block will always access at most worksize+3 elements of data (for scaling=1) it seemed like a good fit. I just tried a single 64x1 workgroup and managed around 60uS with some slightly-broken code: so perhaps the gap could be closed further.

Actually one problem I have is a little more complicated than this anyway: the samples I need to work on are not the base samples, but offset by half a pixel first to produce N+1 of them. With arrays I can use local memory to cache this calculation without having to either run a separate step or do many more lookups: so in this case it will almost certainly end up faster than the image version and I will have to get that local array version working.

For float4 data the images are only about 1.5x faster for this interpolation stuff: which for my problems is not enough to make up for the slower direct access. And the bicubic resampling is also 2-3 slower than the bi-linear, the amount of extra arithmetic is catching up.

Conclusions

Well, about all I conclude is that Nvidia's OpenCL implementation sucks at texture access. I've looked at some of the generated code and each image lookup generates a large chunk of code that appears to be a switch statement. For very big problems most of this can be hidden with overlapped processing but for smaller problems it can be fairly significant. I'm surprised that they, or OpenCL doesn't have some way of telling the compiler that a given image2d_t is always a specific type: the access could be optimised then. FWIW I'm using a driver from a few months ago.

Also I guess: the global memory cache isn't too bad if you have a good regular memory access pattern. Even optimised code that resulted in 4 simple coalesced global memory accesses per thread vs 16 was only a slight improvement.

Of course the other conclusion is that it's a fairly simple problem and no amount of 'cache' optimisation will hide the fact that at some point you still need to go to main memory, for the same amount of data.

I should really do some timings on AMD HW for comparison ... but the computer is in the next room which is also cold and dark.

Final Thought

If you really are doing image stuff with affine transformations and so on, then images are going to win because the access pattern will be regular but it wont be rectangular. The data-types available also match images.

But for scientific computing where you are accessing arrays, images are not going to give you any magical boost on current hardware and can sometimes be more difficult to use. They also add more flexible memory management (e.g. i can use the same memory buffer for smaller or multiple images) and the ability to batch in the 3rd dimension.

LU Decomposition 2

So I finally needed to get that matrix solver working for work ... and revisited the LU decomposition code I had played with a few weeks ago.

It turns out the code was broken, first a simple typo, and then a deeper problem: I hadn't noticed that the loop which multiplies out the rows depends on earlier results. Confusingly of course this worked just fine using a CPU driver since the work items within a work-group are actually executed in serial.

So I had to come up with another solution.

First I wrote a bit of code that just printed out the calculations actually being performed.

For column 0 this amounted to a no-op.

For column 1, it was some edge cases, then something like:

  for i : 0 to n
    col 1 [i] -= col 0 [i] * = col 1 [ 0 ]

For column 2, edge cases plus:

  for i : 0 to n
    col 2 [ i ] -= col 0 [ i ] * col 2 [ 0 ] + col 1 [ i ] * col 2 [ 1 ]

And so on.

As the emboldened calculations depend on a previous iteration of the same loop (for n=1 in case 1, and n=2 in case 2), each column result cannot be calculated independently.

Since the amount of calculation is small, using the shared memory to propagate the partial results didn't seem viable, so instead I simply calculate the required previous values manually for each column for all threads. I fiddled with the code I had which printed out the calculations and turned it into a code generator to expand all loops: it's only a 6x6 matrix so it isn't very much code. For the edge cases I use some logic that zeros out the multiplicands so the entire algorithm is completely branchless.

For example, column 2 is calculated using:

 tmp0 = getlu(lu, 2);
 tmp1 = getlu(lu, 8);
 tmp1 -= getlu(lu, 6) * tmp0;
 tmp0 = cid >= 1 ? tmp0 : 0;
 tmp1 = cid >= 2 ? tmp1 : 0;
 v = getlu(lu, cid * 6 + 2);
 v -= getlu(lu, cid * 6 + 0) * tmp0;
 v -= getlu(lu, cid * 6 + 1) * tmp1;
 barrier(CLK_LOCAL_MEM_FENCE);
 putlu(lu, cid * 6 + 2, v);
 barrier(CLK_LOCAL_MEM_FENCE);
 pivotexchange(lu, piv, 2, cid);
 barrier(CLK_LOCAL_MEM_FENCE);

Where cid is the column id (get_local_id(0) % 6). I use macros to access the array since I am also flattening it out to avoid (or at least reduce) bank conflicts. The barriers are needed since some of the rows span wave-fronts: but in any event only add 3% or so to the processing time.

I've had to write code more than once to understand the data pattern of an algorithm: multi-dimensional array access is bad enough to visualise without adding multi-dimensional processing elements as well. In some cases I've managed to remove huge amounts of redundant calculations this way - matlab seems to encourage code that has very poor data flow for example.

I otherwise stuck to the same thread topology: 6 threads work on each 6x6 matrix together, and 192 threads in the local work group for a total of 32 matrices.

For 4096 solutions of the same 6x6 matrix (i.e. best-case branch divergence), it takes 26uS on the GTX 480. That seems reasonable enough to me. Although I still have a small number of bank conflicts I think this result is good enough for an early minute for today.

Control the Roll

I think I hit a bug in the NVidia OpenCL compiler today, and lost a bit of faith in compilers in general ..

What was a fairly small routine with a simple loop - wanted to use 63 registers/work item. No matter how i tried to unroll the loop using #pragma unroll, re-arrange the work to use vectors or not, and so on.

// local group size = 16, 16, 1
kernel void
somefunc(..., constant float *f0b, ...) {
    local float *localdata[];

    ... load local data ...

    for (int i=0;i<9;i++) {
        float a0 = localdata[i*2];
        float a1 = localdata[i*2+1];
        ...
        v0 += f0a[i*2] * a0 + f1a[i*2] * a1;
        v1 += f0b[i*2] * b0 + f1b[i*2] * b1;
        v2 += f0a[i*2+1] * a0 + f1a[i*2] * a1;
        v3 += f0b[i*2+1] * a0 + f1b[i*2] * b1;
    }
}

Looking at the intermediate code it had about a thousand(!) redundant register moves to/from other registers. For the small problem I had it was taking about 100uS which probably wouldn't have bothered me apart from the weird compiler output.

So I removed the loop entirely by hand, using C macros to implement each step.

Result: 73uS & 21 registers.

And the intermediate code was much smaller and more compact.

NVidia's compiler seems to do a pretty crappy job with vectors in any event, the vector version was even worse - half the speed of a scalar version - around 200uS. It's nor normally this extreme but it seems it's almost always faster not to use vector code. It would also (only sometimes!) hang for 20 seconds or more whilst compiling this file, and these changes fixed that too.