3 pass affine fourier resample
Just an example from the resample stuff I was looking at recently.
Source input - Lenna scaled by 1/8 using imagemagic with a Lanczos filter:
I'm applying an affine matrix with a 7° rotation and a 8x scale in each dimension. Apart from the test algorithm the rest are just using Java2D for the resampling on 8-bit images.
Just to see how little information is present i'll start with the nearest-neighbour version. The ringing at the top of the hat suggests artefacts have been added by the downsampling process.
Now for bilinear, which makes a right pigs breakfast of things:
Then comes bicubic. Which really isn't much better than bilinear once you get to this kind of scale. It's still making a mess of things:
And finally the one which is based on a three-pass shear and/or scale algorithm. It comprises three separate stages.
- Horizontal shear and scale;
- Vertical shear and scale;
- Horizontal shear.
Each operates only in a single dimension which greatly simplifies the resampling required - one only needs to be able to resample and scale in one dimension.
I'm using a trick to avoid the typical sinc filter ringing along the edges of the image itself, and i'm not cropping the result properly yet.
Unfortunately due to using a Fourier Transform for scaling I end up with a bit of ringing primarily due to the Gibbs Phenomenon. How much of this is present depends on the source image too, and even the nearest-neighbour result shows that the Lanczos downsampling has added some ringing to start with.
Even with the ringing certain features are significantly smoother - such as the brim of her hat, top of her shoulder, or the frame of the mirror.
Most of the design including using the Fourier Transform for arbitrary shift/scaling is from the paper Methods for Efficient, High Quality Volume Resampling in the Frequency Domain; Aili Li , Klaus Mueller. But i'm using the affine matrix decomposition in ``Bottleneck-free separable affine image warping''; Owen, C.B. ; Makedon, F. Image Processing, 1997. Proceedings., International Conference on (Volume:1 ). A related paper which just covers rotation is High Quality Alias Free Image Rotation; Charles B. Owen, Fillia Makedon.
Spectral Analysis
Visual appearnce is one thing, but how true to the desired signal is each result mathematically? Taking a log power spectrum of a portion of the image (without edges) allows me to look a bit deeper.
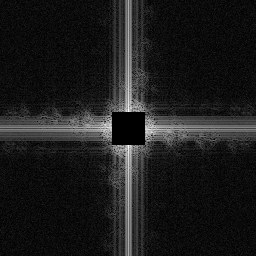
Since i've upscaled by 8x in each dimension an ideal (i.e. sinc filter) resampling will contain no higher frequencies than were originally present - i.e. for a 64x64 image upscaled by any amount, only the lowest 64x64 frequencies should contain any information at all (it will be rotated along with the signal however). To emphasise this I've zeroed out the signal-bearing frequencies in the following spectrograms so that only the distortion added by each algorithm is displayed.
To be "farier" on the 8-bit resampling i've also taken the power spectrum of the quantised 8-bit result of the Fourier based algorithm as used to generate the PNG. This quantisation mostly shows up (?) as noise along the axes.
Note that each spectrum is auto-scaled so the brightness levels do not necessarily represent equivalent amounts of distortion.
To the spectrums ... first the nearest-neighbour. This basically leaks a copy of the original signal as a grid across the whole spectrum.
Bilinear reduces these signal copies significantly apart from along the axes.
Bicubic reduces them further but there is still significant signal leaking out to the adjacent frequencies. Approximately 1.5x along each axis.
And finally the result from the Fourier based method. Apart from the axes which are primarily due to the quantisation to 8-bit (i think), most of the signal is just noise plus a little from the rotation leaking past the mask.