FFT bit-reverse, NEON
Hacked up a NEON version of the FFT permute I mentioned in the last post. Because it worked out much simpler to code up I went with the blocked-8 8-streaming version. Fortunately ARM has a bit-reverse instruction too.
Actually it ended up rather elegant; although i need to use 9 separate addresses within the inner loop, I only need to explicitly calculate one of them. The other 8 are calculated implicitly by a post-increment load thanks to being able to fit all 8 into separate registers. The destination address calculation still needs a bit reversal but 3 instructions are enough to calculate the target address and index to the next one.
This leads to a nice compact loop:
1: rbit r12,r11
add r11,r3
add r12,r1
vld1.64 { d16 },[r0]!
vld1.64 { d17 },[r4]!
vld1.64 { d18 },[r5]!
vld1.64 { d19 },[r6]!
vld1.64 { d20 },[r7]!
vld1.64 { d21 },[r8]!
vld1.64 { d22 },[r9]!
vld1.64 { d23 },[r10]!
subs r2,#1
vstmia r12, {d16-d23}
bne 1b
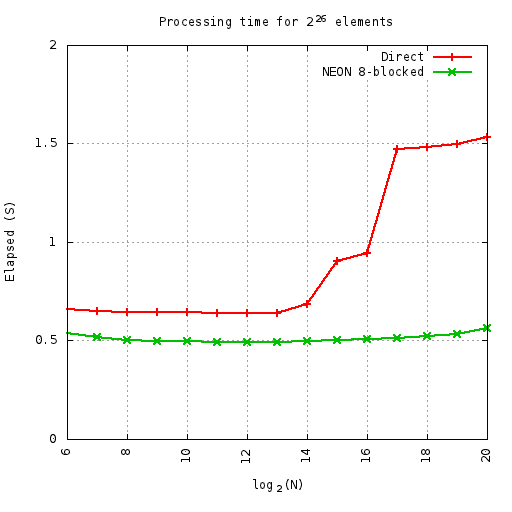
Despite this elegance and simplicity, compared to a straightforward C version the performance is only a bit better until the cache gets overflown.
At least on this machine (parallella-16 - the ARM side) the benefits of the cache-friendly code are measuable and start at 32K elements.
Here i'm runnning so many cycles of the given permute, where the number of cycles x N = 226 - i.e. always doing the same number of total elements. This equates to 1M iterations at 64-elements. All elements are complex float. This means the smaller sizes do more loops than the larger ones - so the small up-tick on the ends is first from extra outer loop overheads, and then from extra inner loop overheads.
Also hit a weird thing with the parallella compiler: by default gcc compiles in thumb mode rather than arm.
Update: So I found out why my profiling attempts were so broken on parallella - the cpu gouverner.
# echo performance > /sys/devices/system/cpu/cpu0/cpufreq/scaling_governor
Fixes that. It also makes emacs a lot smoother (I was wondering why text-mode emacs across a gig-e connection was lagging so much). I was running some timings on a C implementation of Cooley-Tukey and noticed some strange results - it turned out the scheduler was only kicking in once the problem got big enough so time-per-element turned into a saw-tooth.
Actually I re-ran the above plot and although the numbers did change a little bit they were only minor. Oh, I also added alignment specifiers to the vld1 instructions - which made a small but significant difference. I then tried doubling-up on the above function - forming 16 consecutive output cfloat results. But this was consistently slower - I guess hitting 2x the width on output is causing more cache thrashing (although i'm not sure why it's slower when running in-cache).
Some noise woke me up around 2am and I ended up getting up to have something to eat and then hacked until sunrise due to insomnia (pity Sunday is the mowing day around here - so now i'm grumpy and tired and need to do my own noise-making in the back yard soon). I did the timing stuff above and then looked into adding some extra processing to the permute function - i.e. the first couple of stages of the Cooley-Tukey algorithm. NEON has plenty of registers to manage 3 stages for 8 elements but it becomes a pain to shuffle the registers around to be able to take advantage of the wide instructions. So although i've nearly got a first cut done i'm losing interest (although simply being 'tired' makes it easy to become 'tired of' anything) - parallella will remove the need to fuck around with SIMD entirely, and there isn't much point working on a fast NEON FFT when ffts already exists (apart from the for-the-fun-of-it exploration). Well I do have a possible idea for a NEON implementation of a "vertical" FFT which I will eventually explore - the ability to perform the vertical portion of a 2D fft without a transpose could be a win. Because of the data-arrangement this should be easier to implement whilst still gaining the FLOP multiplier of SIMD but there are some other complications involved too.