branchless stackless merge sort

After a previous post I had some other thoughts about implementing a branch-less merge. And further, of removing any stack or recursion as well, at least in certain cases.

This is more of a mental exercise in this case because I only looked at sorting an array - where you're better off using qsort, but it might be worth it on a linked list.

First merge version:

static inline void merge1(void * restrict head1,
     int len1,
     void *tmpData,
     CmpFunc cmp,
     size_t itemsize)
{
 void * restrict tail1 = head1 + len1*itemsize;
 void * restrict head2 = tail1;
 void * restrict tail2 = head2 + len1 * itemsize;

 void * restrict h1 = tmpData;
 void * restrict t1 = tmpData;
 void * restrict tail = head1;

 // copy first array to temporary buffer
 t1 = tmpData + (tail1-head1);
 memcpy(tmpData, head1, tail1-head1+itemsize);

 // merge temporary buffer into target buffer
 while (1) {
  if (cmp(h1, head2) < 0) {
   memcpy(tail, h1, itemsize);
   tail += itemsize;
   if (h1 == t1)
    // end of first list - rest is already in place
    goto done;
   h1 += itemsize;
  } else {
   memcpy(tail, head2, itemsize);
   tail += itemsize;
   if (head2 == tail2) {
    // end of second list - copy rest of first list back
    memcpy(tail, h1, t1-h1+itemsize);
    goto done;
   }
   head2 += itemsize;
  }
 }
 done:
  return;
}

Keeping the loop simple is the best policy in this case.

The branchless merge:

static inline void merge2(void * restrict head1,
     int len1,
     void * restrict tmp,
     CmpFunc cmp,
     size_t itemsize,
     void *sentinel)
{
 void *h1 = tmp;
 void *h2 = head1+len1*itemsize;
 void *out = head1;
 int len = len1*2;
 int i;

 // copy first half array to temporary buffer & add sentinal
 memcpy(tmp, head1, len1*itemsize);
 memcpy(tmp+len1*itemsize, sentinel, itemsize);

 // save spot for sentinel in 2nd array
 memcpy(tmp+len1*itemsize+itemsize, h2+len1*itemsize, itemsize);
 memcpy(h2+len1*itemsize, sentinel, itemsize);

 // merge
 for (i=0;i<len;i++) {
  int c;

  c = cmp(h1, h2) < 0;  
  memcpy(out, c ? h1 : h2, itemsize);
  h1 = c ? h1 + itemsize : h1;
  h2 = c ? h2 : h2 + itemsize;
  out += itemsize;
 }

 // restore
 memcpy(h2+len1*itemsize, tmp+len1*itemsize+itemsize, itemsize);
}

It uses a sentinel so there needs to be no testing of loop termination beyond the number of total elements being merged.

And finally the removal of the stack or recursion to find out when merges need to take place. One simple way (breadth-first) is just to iterate over the whole array, at size 2, then 4, 8, and so on, but this has poor locality of references. So this simple logic is used to track when and how large merges are to take place and does them in a depth-first fashion.

void MergeSort(void *data, size_t count, size_t itemsize, CmpFunc cmp, void *sentinal) {
 int i, j;
 int last = 0;
 void *tmp;

 tmp = malloc((count+1) * itemsize);

 for (i=0;i<count;) {
  batchers8(data+i*itemsize, tmp, cmp, itemsize);
  i += 8;
  for (j=16;j<=count;j<<=1) {
   if (j&(i^last)) {
    merge2(data+(i-j)*itemsize, j/2, tmp, cmp, itemsize, sentinal);
   }
  }
  last = i;
 }

 free(tmp);
}

This code also performs the bottom sort in 8 element lots using an unrolled batchers sort. So one might note that this particular sort is limited to sorting arrays whose number of elements is a power of 2 ...

I ran a few timings and this is slightly faster than the natural merge sort that I had previously written in certain cases - that of course is still much faster for the already-sorted case. The version I timed had the merge step manually unrolled 8 times as well.

For random input, the branchless merge is about 10% faster than the original merge, and the original merge is about 10% faster than my original natural merge sort. So the lack of conditional execution ends up a bonus, even considering the extra overheads, and all the extra memory moves. This is on an intel cpu anyway - which is so register starved they've had to make such code run fast, so one might not end up with the same result on other architectures.

There is more possible here too if you're sorting basic types (i.e. not a general interface as above) - all of these algorithms can be vectorised to run on SIMD processors. It could for example independently sort 4 interleaved arrays in the same number of operations, and then merge those in 2-3 passes at the end (or 1, with a 4-way merge).

Sentinels are a pretty nice optimisation trick but they usually require some sort of extra housekeeping that makes their use impractical. For example in the camel-mime-parser code I used a sentinel of \n at the end of the i/o buffer every time i refreshed it so the lowest level loop which identified individual lines was only 3 instructions long - and it only checked for running out of input after the loop had terminated. But I had to write my own i/o buffering to have such control of the memory.

putAcquireGLObject()

Damnit, i've done it again. That's what I get for trying to cut and paste some old code that apparently never worked anyway.

I was trying to implement an OpenGL rendering loop for some OpenCL code rather than copying it back to Java2D every time. Except I based the code on some test code i'd written which now I realise never worked.

And mostly it failed because it didn't call putAcquiteGLObject() before writing to the output texture.

A few more hours of my day i'll never get back ... and I think it's the second time i've done it. Maybe i'll remember it this time if I write it down.

More sort thoughts

Late last night when I should really have already headed to bed I had some more thoughts on the median filter and played a bit with a batchers sort generator.For a 9 value median, rather than do a full 9 element sort, one could just do an 8 element sort and then attempt to insert the final value into the middle. The insert which only must be valid for the centre value only takes 2 additional cas steps. But an 8 sort takes quite a few fewer steps than a 9 sort, and even then 2 are redundant for finding the median. In short, this allows a 9 element median to be calculated in only 19 cas operations rather than 22.

For larger sorts one can probably repeat the process further.

3x3 median filter, or branchless loopless sort

So while thinking of something I could add to socles to make it worth uploading I thought of implementing a median filter.

Median filters are a bit of a pain because one has to sort all of the pixel values (for a greyscale image at least) before getting the result - and sorts generally require loops and other conditional code which make things a bit inefficient when executed on a GPU.

So somehow i'm back to looking into sorts again ... the never-ending quest continues.

Fortunately, this is another case where a batchers sort or other hand-rolled sorting networks come to the rescue. And since each element is being processed independently there are no inter-thread dependencies and all the processing can be unrolled and performed on registers (if you have enough of them).

So I implemented the 9 element sorting network from Knuth Volume 3 section 5.3.4 which sorts 9 elements in 25 compare and swap steps. But since 3 of the comparisons of the 25 aren't involved in the median value I also dropped them and ended up with 22 inline comparison and swaps to find the median value. Fortunately this is a small enough problem to fit entirely into registers too.

This also works pretty well in C - an albeit-inline version - manages to perform 100M median calculations on a 9 integer array (on the same array which is copied over) in 1.26s on my workstation, using the glibc qsort() to do the same task takes 17s. (I didn't verify that the inline version was transferring data to/from memory as it should in the micro-benchmark, but that does sound about right all things considered).

So, given unsorted values s0-s8, and an operator cas(a, b) (compare and swap) which results in a < b, the median can be calculated using the following 22 steps:

        cas(s1, s2);
        cas(s4, s5);
        cas(s7, s8);

        cas(s0, s1);
        cas(s3, s4);
        cas(s6, s7);

        cas(s1, s2);
        cas(s4, s5);
        cas(s7, s8);

        cas(s3, s6);
        cas(s4, s7);
        cas(s5, s8);
        cas(s0, s3);

        cas(s1, s4);
        cas(s2, s5);
        cas(s3, s6);

        cas(s4, s7);
        cas(s1, s3);

        cas(s2, s6);

        cas(s2, s3);
        cas(s4, s6);

        cas(s3, s4);

s4 now contains the median value. cas can be implemented using 1 compare and 2 selects.

But perhaps the nicest thing is the code is directly vectorisable.

Some timings using a 4 channel 32-bit input image 640x480 and producing a 4 channel 32-bit output image: For 1 element it takes 84uS, for 3 elements 175uS and 4 elements 238uS. This is on a NVidia 480GTX.

The current implementation: median.cl.

socles

I finally started a new project to store some of the simpler OpenCL stuff i've been working on.I've called it socles - a socle is another word for plynth - the base of a column.

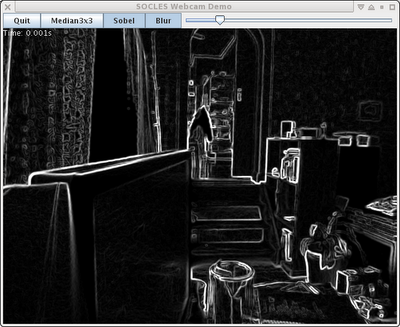
It's a really basic set of operations at the moment, but I hope they are decent implementations thereof at least.

Convolved out

Bit of a dry post coming up, but when you consider I blew my Sunday on this it might make sense. Curiosity got the better of me today and I spent most of it playing with convolutions with OpenCL on a GPU - I had a pretty fast implementation but wanted to compare it with some other ideas I had.

As it turned out, the implementation I had was the fastest after-all, although I tweaked it a tiny bit during the process.

For kernels at 3x3 (or 7x7 for 4-channel UBYTE images), a simple 2d implementation is very slightly faster than a more complex algorithm.

For non-separable convolution, a complex implementation which uses a rolling buffer is over 3x faster than a naive implementation, at least up to sizes of 31x31.

For separable convolution, my complex implementation is up to 2.5x faster than a naive implementation.

My separable convolution implementation reads 16x16 blocks of image into local memory and then each thread generates all results from the local memory in one pass - e.g. for up to 7x7 convolution it reads 2x16x16 blocks, for up to 15x15 convolution it reads 3x16x16 blocks, and so on i.e. you need the 16x16 data plus 'kernel radius' pixels each size. It uses transpose for the Y convolution case during load and saving of the data but the processing is identical. It also uses the trick of offsetting the odd rows of the data so they avoid local memory contention when they might otherwise - e.g. when the number of bocks being read is even.

FWIW for 640x480 image on a GTX 480 A single channel FLOAT 31x31 separable convolution is about 190uS, or 470uS for naive version. For UBYTE 177uS vs 470uS. For a 4 channel image the timings are 413uS, 916uS, 389uS, and 465uS respectively. So larger (byte size) images gain more - presumably from the reduction in memory reads and lower cache loading.

Actually - yesterday I started working on a JOCL based image processing library that I intend to drop on google code at some point - and this investigation was part of that. More should be forthcoming on that soon although right now I just don't have enough put together to be much use.

Luser error

So it turns out the main problem with the performance issues in my last post wasn't the cache being overloaded after all ... but the compiler running out of registers to unroll a couple of nested loops I asked it to.

It turns out because of a cut and paste job I left in some test code which was limiting the register count for the compiler, and the register spillage was a bit of a disaster and causing the order of magnitude drop. With this fixed things look a lot more promising, although at ~4ms it is still a little slower than I would like and I can't see much being able to be done to improve it.

It's a bit weird that an unconstrained compile for a specific device would choose to use all registers it needs for the code-unrolling, ignoring the device specifics, but I guess this is some particular of the nvidia opencl implementation.

There is still some problems with the texture cache being hit too hard anyway - the integral image has to be stored using the UINT32 data type, and it needs at least 8 lookups per feature tested which is a pretty heavy load to start with. With the other feature tester I could just use 8 bit images which fits better into the cache it seems (contrary to what i'd believed until this point).

Investigations ongoing ...

Cache only works when there's enough

Update: Seems I was (mostly) wrong - see the follow-up post.

I've been playing with object classifiers in OpenCL - I have one that works, not terribly well but relatively quickly. It's a random tree classifier and just uses pixel intensity comparisons for feature tests. Although I can get some results out of it they just weren't reliable enough.

So I decided to use 2-bit-binary patterns instead, a haar-like feature measure which uses an integral image to accelerate the intensity comparisons (maybe more on the integral image creation another time, that was a bit of a journey in OpenCL as well). Unfortunately the simple modifications required to change the feature detector suddenly blew out the computation time - from under 1ms to over 20ms, making it far too slow. This even though it only requires twice the memory accesses for the same number of tests.

After much experimentation I found the cause - the texture cache was being exhausted, dramatically reducing the apparent memory throughput. I discovered that a single-tree, 3-feature tester is about the limit of the texture cache. That will execute in 150uS. 4-features take 250uS, and if I change the 4-feature system to 2 trees, or 8 features - just twice the amount of work - it blows out to 1500uS.

Well, at least that gives me options for splitting the work into multiple passes and maybe i'll end up with something fast enough over-all. Otherwise I might have to find something else. As it is i'm losing confidence that it is going to be good enough anyway (maybe after running it so many times i've forgotten how poor the previous one was).