Viola & Jones Detector OpenCL

After being a bit distracted yesterday evening by my co-dwellers, I got stuck into a problem I've been wanting to look at for a while - running a Viola & Jones cascade detector on the GPU using OpenCL. I'd just got an integral image calculator done so was eager to use it.I've had a few goes in the past but always seemed to mess up some of the weighting calculations, so I started with the code from OpenClooVision which is a bit easier to follow than the OpenCV implementation, although could certainly use some work.

So, by about 6am I had a working implementation ... but it was really very slow. Far too slow to even consider for what I need, and worse, it doesn't scale at all well - running it on smaller problem sizes just makes it even less efficient.

Who is that fat bastard?

I went to bed shivering cold but mostly wondering just what I could do to speed it up. I have previously done some work with integral images, and I found they do not work particularly well on GPUs - even calculating them aside (which I managed to solve with an acceptable solution although it took many many dead-ends and grey hairs). Although on paper they look like an efficient solution - a handful of array lookups to calculate an area sum - in use they seem to interact poorly with texture cache.

It was taking in excess of 30 000uS to perform 14 passes on a 640x480 test image in steps of 5 with a scale of 1.25.

The OpenCV and faint implementations both pre-scale the features and feature-weights. I never quite understood why until I had a working implementation, and the OpenClooVision version was calculating them on the fly. So the first stop was to try this. Pre-calculating the weights is extremely cheap, and this lead to around a 50% performance boost.

I still had a problem with the GPU hardly being utilised, particularly at the larger scales (fewer tasks/call) or with smaller images. And because each thread was working on a separate probe, there was very little coherency in processing or data.

However, I noticed that for the cascade I was using (the default one from OpenCV) it was running many feature tests for each stage - 25-200; and that calculating the feature value was unconditional - something ripe for parallelisation.

So I tried launching 64 threads for each probe location, and they work together on the list of features in blocks of 64, and then tally them up at the end using thread 0. This was the biggest improvement and I managed to get it down to around 12 000uS.

I then tried a parallel prefix sum - which got it down to about 11 000uS, although then I tried a sqrt(N) sum (split the summation into 2 passes, first 16 threads produce 16 partial sums, then 1 thread adds those up) and got it down to about 10 500uS. Parallel prefix sum loses again.

And then to cut a long story short I tried a whole bunch of variations, such as storing the regions in integer format - this made it faster, but only because it wasn't calculating the same results. And different work-sizes - 64 worked the best. And different packing formats for the feature descriptors. But no matter what I tried, about 10 500 uS was about the best I could manage with the test image.

I also tried a slightly modified version (no thread dependencies) running on the AMD CPU driver, on the 6 core+HT machine I have. That managed 90mS. So the GPU is only 10x faster, which although nothing to sneeze at is still a bit disappointing.

To me this is still a little on the slow side, but I'm pretty much out of ideas for now. It might just be a problem that defies any particularly efficient mapping to GPU hardware.

Actually one thing I haven't tried is scaling the images instead of the features ... but I think that's something that can wait for another day.

OpenCL Kanade Lucas Tomasi feature tracking

I've added a couple of things to socles, the main being an implementation of Kanade Lucas Tomasi feature tracking. It's just a fairly simple translation of the public domain version here (site seems down at time of writing), with a few tweaks for good GPU performance. Ok it looks nothing like it, but all i did was remove the need for 3 temporary images and the loops to create and use them by noting that each element was independent of the other and so they could all be moved inside of a single loop.

I've only implemented the translation-only version of the tracker, with the lighting-sensitive matching algorithm. The affine version shouldn't be terribly difficult - it's mostly just re-arranging the code in a similar fashion (although the 6x6 matrix solver might benefit from more thorough work).

Really awful screenshot of it in action ... (it's very late again)

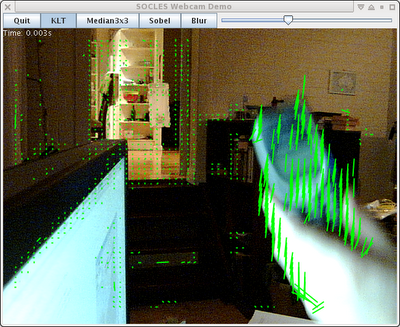
The 3300 regularly spaced feature points above take about 1.5ms to track in GPU time (480 GTX), including all of the image pyramid and gradient image set-up for the incoming frame. It uses 3 levels of pyramid with each 1/4 the size in each dimension of the one below. Most of the points lose track because there isn't enough detail to meet the quality settings, hence the areas with no green dots.

With a CPU implementation the majority of the time is taken in the convolutions necessary to setup the image pyramid - although eventually with enough features one reaches a break-even point. In this case it's about 500uS for the image setup for 640x480 image (3 convolutions at full res, 2 at each subsampling and one resample), and 1ms for the 3300 tracks (i.e. 0.3 microsecond per additional 16x16 feature tracked). Well that's quick enough to keep me happy anyway. At least for now!

I implemented this using a pattern which I've found after much (much) trial and error to be reliably efficient for mapping many types of rectilinear problems to GPU processes, which i'll just call an NxM execution pattern. For a feature-size of 'NxM', the code assigns 'N' threads to each feature, each which works on a column of 'M' rows of data, with the first thread in the sub-group used to tally results and make decisions. A small amount of local memory is used for the partial sums and to share the decisions amongst the threads. These are mapped to a flat work size which is independent of the local workgroup size, which allows for easy tuning adjustments. So a feature size of 9 would be mapped using 7 features if the local work-size is 64, with 15 threads idle (i.e. choose factors of the worksize for best efficiency, but it can still work well with any size). 100 such features would need 15 work groups (ceil(100/7)). The address arithmetic is a bit messy but it only needs to be calculated once on entry, after that it is simple fixed indexing. And since you can reference any memory/local memory by local id 0 you don't have to worry about memory bank conflicts.

I tried many other variations of mapping the work to the GPU and this was by far the best (and not far off the simplest once the fiddly address calculations are out of the way). For example, using a parallel prefix some across all elements with a 3d work size (i.e. 16x16xnfeatures) was about 1/2 the speed IIRC - the increased parallelism was a hindrance because of both the IPC required and the over-utilisation of resources (more local memory and threads).

Update Ok I found a pretty major problem with this mapping of the jobs - early exit of some sub-workgroups messes up the barrier usage which upsets at least the AMD cpu driver. So all threads need to keep executing until they are all finished and then mask the result appropriately, which will complicate matters but hopefully not by much.Update 2 I think I managed to solve it, although I had some trouble with the code behaving as I expected, and got misled by bugs in other kernels.

branchless stackless merge sort

After a previous post I had some other thoughts about implementing a branch-less merge. And further, of removing any stack or recursion as well, at least in certain cases.

This is more of a mental exercise in this case because I only looked at sorting an array - where you're better off using qsort, but it might be worth it on a linked list.

First merge version:

static inline void merge1(void * restrict head1,
     int len1,
     void *tmpData,
     CmpFunc cmp,
     size_t itemsize)
{
 void * restrict tail1 = head1 + len1*itemsize;
 void * restrict head2 = tail1;
 void * restrict tail2 = head2 + len1 * itemsize;

 void * restrict h1 = tmpData;
 void * restrict t1 = tmpData;
 void * restrict tail = head1;

 // copy first array to temporary buffer
 t1 = tmpData + (tail1-head1);
 memcpy(tmpData, head1, tail1-head1+itemsize);

 // merge temporary buffer into target buffer
 while (1) {
  if (cmp(h1, head2) < 0) {
   memcpy(tail, h1, itemsize);
   tail += itemsize;
   if (h1 == t1)
    // end of first list - rest is already in place
    goto done;
   h1 += itemsize;
  } else {
   memcpy(tail, head2, itemsize);
   tail += itemsize;
   if (head2 == tail2) {
    // end of second list - copy rest of first list back
    memcpy(tail, h1, t1-h1+itemsize);
    goto done;
   }
   head2 += itemsize;
  }
 }
 done:
  return;
}

Keeping the loop simple is the best policy in this case.

The branchless merge:

static inline void merge2(void * restrict head1,
     int len1,
     void * restrict tmp,
     CmpFunc cmp,
     size_t itemsize,
     void *sentinel)
{
 void *h1 = tmp;
 void *h2 = head1+len1*itemsize;
 void *out = head1;
 int len = len1*2;
 int i;

 // copy first half array to temporary buffer & add sentinal
 memcpy(tmp, head1, len1*itemsize);
 memcpy(tmp+len1*itemsize, sentinel, itemsize);

 // save spot for sentinel in 2nd array
 memcpy(tmp+len1*itemsize+itemsize, h2+len1*itemsize, itemsize);
 memcpy(h2+len1*itemsize, sentinel, itemsize);

 // merge
 for (i=0;i<len;i++) {
  int c;

  c = cmp(h1, h2) < 0;  
  memcpy(out, c ? h1 : h2, itemsize);
  h1 = c ? h1 + itemsize : h1;
  h2 = c ? h2 : h2 + itemsize;
  out += itemsize;
 }

 // restore
 memcpy(h2+len1*itemsize, tmp+len1*itemsize+itemsize, itemsize);
}

It uses a sentinel so there needs to be no testing of loop termination beyond the number of total elements being merged.

And finally the removal of the stack or recursion to find out when merges need to take place. One simple way (breadth-first) is just to iterate over the whole array, at size 2, then 4, 8, and so on, but this has poor locality of references. So this simple logic is used to track when and how large merges are to take place and does them in a depth-first fashion.

void MergeSort(void *data, size_t count, size_t itemsize, CmpFunc cmp, void *sentinal) {
 int i, j;
 int last = 0;
 void *tmp;

 tmp = malloc((count+1) * itemsize);

 for (i=0;i<count;) {
  batchers8(data+i*itemsize, tmp, cmp, itemsize);
  i += 8;
  for (j=16;j<=count;j<<=1) {
   if (j&(i^last)) {
    merge2(data+(i-j)*itemsize, j/2, tmp, cmp, itemsize, sentinal);
   }
  }
  last = i;
 }

 free(tmp);
}

This code also performs the bottom sort in 8 element lots using an unrolled batchers sort. So one might note that this particular sort is limited to sorting arrays whose number of elements is a power of 2 ...

I ran a few timings and this is slightly faster than the natural merge sort that I had previously written in certain cases - that of course is still much faster for the already-sorted case. The version I timed had the merge step manually unrolled 8 times as well.

For random input, the branchless merge is about 10% faster than the original merge, and the original merge is about 10% faster than my original natural merge sort. So the lack of conditional execution ends up a bonus, even considering the extra overheads, and all the extra memory moves. This is on an intel cpu anyway - which is so register starved they've had to make such code run fast, so one might not end up with the same result on other architectures.

There is more possible here too if you're sorting basic types (i.e. not a general interface as above) - all of these algorithms can be vectorised to run on SIMD processors. It could for example independently sort 4 interleaved arrays in the same number of operations, and then merge those in 2-3 passes at the end (or 1, with a 4-way merge).

Sentinels are a pretty nice optimisation trick but they usually require some sort of extra housekeeping that makes their use impractical. For example in the camel-mime-parser code I used a sentinel of \n at the end of the i/o buffer every time i refreshed it so the lowest level loop which identified individual lines was only 3 instructions long - and it only checked for running out of input after the loop had terminated. But I had to write my own i/o buffering to have such control of the memory.

putAcquireGLObject()

Damnit, i've done it again. That's what I get for trying to cut and paste some old code that apparently never worked anyway.

I was trying to implement an OpenGL rendering loop for some OpenCL code rather than copying it back to Java2D every time. Except I based the code on some test code i'd written which now I realise never worked.

And mostly it failed because it didn't call putAcquiteGLObject() before writing to the output texture.

A few more hours of my day i'll never get back ... and I think it's the second time i've done it. Maybe i'll remember it this time if I write it down.

More sort thoughts

Late last night when I should really have already headed to bed I had some more thoughts on the median filter and played a bit with a batchers sort generator.For a 9 value median, rather than do a full 9 element sort, one could just do an 8 element sort and then attempt to insert the final value into the middle. The insert which only must be valid for the centre value only takes 2 additional cas steps. But an 8 sort takes quite a few fewer steps than a 9 sort, and even then 2 are redundant for finding the median. In short, this allows a 9 element median to be calculated in only 19 cas operations rather than 22.

For larger sorts one can probably repeat the process further.

3x3 median filter, or branchless loopless sort

So while thinking of something I could add to socles to make it worth uploading I thought of implementing a median filter.

Median filters are a bit of a pain because one has to sort all of the pixel values (for a greyscale image at least) before getting the result - and sorts generally require loops and other conditional code which make things a bit inefficient when executed on a GPU.

So somehow i'm back to looking into sorts again ... the never-ending quest continues.

Fortunately, this is another case where a batchers sort or other hand-rolled sorting networks come to the rescue. And since each element is being processed independently there are no inter-thread dependencies and all the processing can be unrolled and performed on registers (if you have enough of them).

So I implemented the 9 element sorting network from Knuth Volume 3 section 5.3.4 which sorts 9 elements in 25 compare and swap steps. But since 3 of the comparisons of the 25 aren't involved in the median value I also dropped them and ended up with 22 inline comparison and swaps to find the median value. Fortunately this is a small enough problem to fit entirely into registers too.

This also works pretty well in C - an albeit-inline version - manages to perform 100M median calculations on a 9 integer array (on the same array which is copied over) in 1.26s on my workstation, using the glibc qsort() to do the same task takes 17s. (I didn't verify that the inline version was transferring data to/from memory as it should in the micro-benchmark, but that does sound about right all things considered).

So, given unsorted values s0-s8, and an operator cas(a, b) (compare and swap) which results in a < b, the median can be calculated using the following 22 steps:

        cas(s1, s2);
        cas(s4, s5);
        cas(s7, s8);

        cas(s0, s1);
        cas(s3, s4);
        cas(s6, s7);

        cas(s1, s2);
        cas(s4, s5);
        cas(s7, s8);

        cas(s3, s6);
        cas(s4, s7);
        cas(s5, s8);
        cas(s0, s3);

        cas(s1, s4);
        cas(s2, s5);
        cas(s3, s6);

        cas(s4, s7);
        cas(s1, s3);

        cas(s2, s6);

        cas(s2, s3);
        cas(s4, s6);

        cas(s3, s4);

s4 now contains the median value. cas can be implemented using 1 compare and 2 selects.

But perhaps the nicest thing is the code is directly vectorisable.

Some timings using a 4 channel 32-bit input image 640x480 and producing a 4 channel 32-bit output image: For 1 element it takes 84uS, for 3 elements 175uS and 4 elements 238uS. This is on a NVidia 480GTX.

The current implementation: median.cl.

socles

I finally started a new project to store some of the simpler OpenCL stuff i've been working on.I've called it socles - a socle is another word for plynth - the base of a column.

It's a really basic set of operations at the moment, but I hope they are decent implementations thereof at least.

Convolved out

Bit of a dry post coming up, but when you consider I blew my Sunday on this it might make sense. Curiosity got the better of me today and I spent most of it playing with convolutions with OpenCL on a GPU - I had a pretty fast implementation but wanted to compare it with some other ideas I had.

As it turned out, the implementation I had was the fastest after-all, although I tweaked it a tiny bit during the process.

For kernels at 3x3 (or 7x7 for 4-channel UBYTE images), a simple 2d implementation is very slightly faster than a more complex algorithm.

For non-separable convolution, a complex implementation which uses a rolling buffer is over 3x faster than a naive implementation, at least up to sizes of 31x31.

For separable convolution, my complex implementation is up to 2.5x faster than a naive implementation.

My separable convolution implementation reads 16x16 blocks of image into local memory and then each thread generates all results from the local memory in one pass - e.g. for up to 7x7 convolution it reads 2x16x16 blocks, for up to 15x15 convolution it reads 3x16x16 blocks, and so on i.e. you need the 16x16 data plus 'kernel radius' pixels each size. It uses transpose for the Y convolution case during load and saving of the data but the processing is identical. It also uses the trick of offsetting the odd rows of the data so they avoid local memory contention when they might otherwise - e.g. when the number of bocks being read is even.

FWIW for 640x480 image on a GTX 480 A single channel FLOAT 31x31 separable convolution is about 190uS, or 470uS for naive version. For UBYTE 177uS vs 470uS. For a 4 channel image the timings are 413uS, 916uS, 389uS, and 465uS respectively. So larger (byte size) images gain more - presumably from the reduction in memory reads and lower cache loading.

Actually - yesterday I started working on a JOCL based image processing library that I intend to drop on google code at some point - and this investigation was part of that. More should be forthcoming on that soon although right now I just don't have enough put together to be much use.