A better, faster sincos/cexpi

After posting about the fft implementation i've been working on to the parallella forums one kind fellow-hacker directed me to a tool which can be used to improve the error of polynomial estimates to functions. Basically to get the same or better result in fewer terms.

This gave me something to poke at for a couple of evenings but to be honest my maths skills are up shit creek these days and I had trouble working out a good approximation to cosine() or properly forming the expressions to take account of floating point precision limits.

So armed with knowledge of this new technique I did further searching and came across a few interesting papers/presentaitons from the PS2 era about function optimisation and floating point errors and then came across exactly the tool I was after sollya. So I compiled that up and had a bit of a play.

Once I worked out how it worked I did some analysis on the functions I created using lolremez, the ones I had, and some others I found on the net.

First, the 6-term expression I started with. SG(x) here casts the value to a float (C type).

> Z6=x*(SG(3.1415926535897931159979634685441851615906e+00) 
        + x^2 * (SG(-5.1677127800499702559022807690780609846115e+00)
        + x^2 * (SG(2.5501640398773455231662410369608551263809e+00)
        + x^2 * (SG(-5.9926452932079210533800051052821800112724e-01)
        + x^2 * (SG( 8.2145886611128232646095170821354258805513e-02)
        + x^2 * SG(-7.3704309457143504444309733969475928461179e-03))))));
Warning: Rounding occurred when converting the constant "3.1415926535...
Warning: Rounding occurred when converting the constant "5.1677127800...
Warning: Rounding occurred when converting the constant "2.5501640398...
Warning: Rounding occurred when converting the constant "5.9926452932...
Warning: Rounding occurred when converting the constant "8.2145886611...
Warning: Rounding occurred when converting the constant "7.3704309457...
> dirtyinfnorm(sin(x * pi)-Z6, [0;1/4]);
2.32274301387587407010080506217793120115302759634118e-8

Firstly - those float values can't even be represented in single precision float - this is despite attempting to do just that. Given the number of terms, the error rate just isn't very good either.

I used lolremez to calculate a sinf() function with 4 terms, and then analysed it in terms of using float calculations.

> RS = x * ( SG(9.999999861793420056608460221757732708227e-1)
               + x^2 * (SG(-1.666663675429951309567308244260188890284e-1)
               + x^2 * (SG(8.331584606487845846198712890758361670071e-3)
               + x^2 * SG(-1.946211699827310148058364912231798523048e-4))));
Warning: Rounding occurred when converting the constant "9.9999998617...
Warning: Rounding occurred when converting the constant "1.6666636754...
Warning: Rounding occurred when converting the constant "8.3315846064...
Warning: Rounding occurred when converting the constant "1.9462116998...
> dirtyinfnorm(sin(x)-RS, [0;pi/4]);
9.0021097355521826457692679614674224316870784965529e-9

This is roughly 8x the error rate reported by lolremez or sollya with extended precision, but obviously an improvement over the taylor series despite using only 4 terms.

So using sollya to calculate an expression with the same terms whilst forcing the values to be representable in float is very simple.

> LS4 = fpminimax(sin(x), [|1,3,7,5|], [|single...|],[0x1p-16000;pi/4]);
> LS4;
x * (1
     + x^2 * (-0.1666665375232696533203125
     + x^2 * (8.332121185958385467529296875e-3
     + x^2 * (-1.951101585291326045989990234375e-4))))
> dirtyinfnorm(sin(x)-LS4, [0;pi/4]);
2.48825949986510374795541070830762114197913817795157e-9

So ... yep that's better. (0x1p-16000 is just a very small number since the calculation fails for 0.0).

One of the most accurate other implementations I found for sin() was from an article "Faster Math Functions" by Robin Green of Sony (cira ps2 era). The first term of this function is exactly representable in float and the constants calculated using remez. I analysed this in sollya.

> RGS = x * (1 + x^2 * (SG(-0.166666567325592041015625) + x^2 * (SG(0.00833220803) + x^2 * SG(-0.000195168955))));
Warning: Rounding occurred when converting the constant "0.0083322080...
Warning: Rounding occurred when converting the constant "0.0001951689...
> dirtyinfnorm(sin(x)-RGS, [0;pi/4]);
3.40294295123115698469497312067470829353049357459609e-9

Note that the first term is represented in floating point exactly.

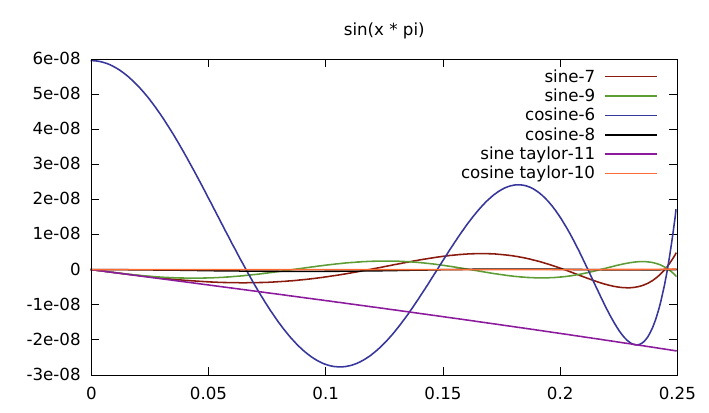
Plot time.

The lolremez version is faltering here because the first term is actually 1 in float, yet the optimisation process is assuming it has much higher accuracy and adjusting the other polynomial exponents appropriately.

> SG(9.999999861793420056608460221757732708227e-1);
1

I did some further mucking about with the tutorial which explained how to fix the first-term into one representable by floats (i.e. 1.0) but I wont include it here since it was superseded by the results from sollya with much less work (i.e. the result above). The one from the Robin Green article should be much the same anyway as it was derived in a similar manner.

cexpi()

So applying the problem to the one I was interested in - sin/cos with an integer argument, leads to the following solutions. By scaling the input value by pi, the full range is normalised to a 1.0, and powers-of-two fractions of one (as required by an fft) can be represented in float with perfect accuracy which removes some of the error during calculation.

> S4 = fpminimax(sin(x * pi), [|1,3,7,5|], [|24...|],[0x1p-16000;1/4]);
> S4;
x * (3.1415927410125732421875
  + x^2 * (-5.16771984100341796875
  + x^2 * (2.550144195556640625
  + x^2 * (-0.592480242252349853515625))))
> C5 = fpminimax(cos(x * pi), [|0,2,4,6,8|], [|24...|],[0;1/4]);
> C5;
1 + x^2 * (-4.93480205535888671875
  + x^2 * (4.0586986541748046875
  + x^2 * (-1.33483588695526123046875
  + x^2 * 0.22974522411823272705078125))) 

The reason for using 4 terms for sine and 5 for cosine is because at least 5 are needed for cosine for similar accuracy and it also creates a matching number of instructions since sine() needs the extra multiply by x - this also improves the instruction scheduling. Using more terms for sine only increases the accuracy by a small bit because this is hitting the limits of floating point accuracy so isn't worth it.

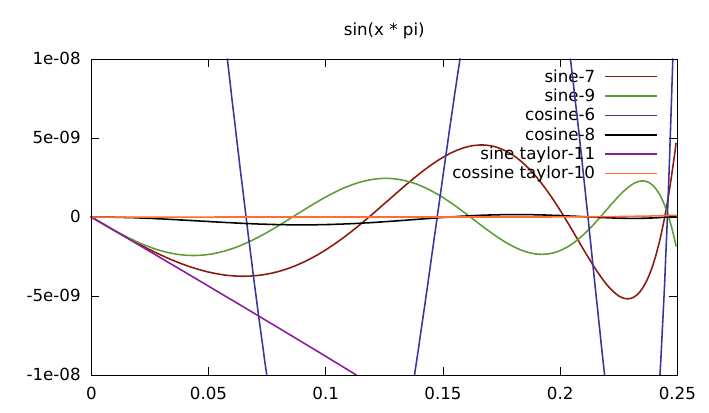
A closer view:

The taylor series for cosine is much better than the one for sine.

fmadd, fmul, etc

Most of the function can be implemented using multiply+add instructions if it is represented in the obvious 'Horner' form.

s = a A + a^3 B + a^5 C + a^7 D
  = a (A + a^2 (B + a^2 (C + a^2 D)

c = 1 + a^2 A + a^4 B + a^6 C + a^8 D
  = 1 + a^2 (A + a^2 (B + a^2 (C + a^2 D)

seq  caclulation
  0  a2 = a * a

  1  s =  2.550144195556640625      + a2 * -0.592480242252349853515625
  1  c = -1.33483588695526123046875 + a2 *  0.22974522411823272705078125

  2  s = -5.16771984100341796875    + a2 * s
  2  c =  4.0586986541748046875     + a2 * c

  3  s = 3.1415927410125732421875   + a2 * s
  3  c = -4.93480205535888671875    + a2 * c

  4  s =                               a * s
  4  c = 1.0                        + a2 * c

Another way to represent the expression is using Estrin's method. I found this mentioned in the stuff by R.Green and he references Knuth.

This breaks the expression into independent sub-trees which can be calculated concurrently. This is obviously quite useful for SIMD calculations but can also be useful on a serial processor with a deep pipeline as it reduces the number of stages with serial dependencies.

s = a A + a^3 B + a^5 C + a^7 D
  = a ( (A + a^2B) + a^4 (C + a^2 D) )

c = 1 + a^2 A + a^4 B + a^6 C + a^8 D
  = 1 + a^2 ( (A + a^2 B) + a^4 (C + a^2 D) )

 seq  calculation

   0  a2 =       a * a

   1  a4 =      a2 * a2
   1  s0 =  A + a2 * B
   1  s1 =  C + a2 * D
   1  c0 =  A + a2 * B
   1  c1 =  C + a2 * D

   2  s3 = s0 + a4 * s2
   2  c3 = c0 + a4 * c2

   3  s  =       a * s3
   3  c  =  1 + a2 * c3

This requires 1 more floating point instruction: but it executes in 3 stages of dependent results rather than 4. If latency of the calculation is important or if there are no other instructions that can be scheduled to fill the latency slots of the fpu instructions this would execute faster.

Exact floats: Hex Float Notation

Whilst looking through some code I came across the hexadecimal float notation which I hadn't seen before. I've been wondering how to correctly encode floating point values with exact values so this I guess is the way.

Sollya can output this directly which is nice, so the above expressions can also be represented (in C) as:

> display = hexadecimal;
Display mode is hexadecimal numbers.
> S4;
x * (0x3.243f6cp0
  + x^0x2.p0 * (-0x5.2aefbp0
  + x^0x2.p0 * (0x2.8cd64p0
  + x^0x2.p0 * (-0x9.7acc9p-4))))
> C5;
0x1.p0
  + x^0x2.p0 * (-0x4.ef4f3p0
  + x^0x2.p0 * (0x4.0f06ep0
  + x^0x2.p0 * (-0x1.55b7cep0
  + x^0x2.p0 * 0x3.ad0954p-4)))

So the hex number is the mantissa, and the exponent is relative to the decimal point in bits. It wont output expressions in IEE754 encoded values directly but they can be printed (useful for assembly).

> printsingle( 0x3.243f6cp0);
0x40490fdb
> printsingle(3.1415927410125732421875);
0x40490fdb

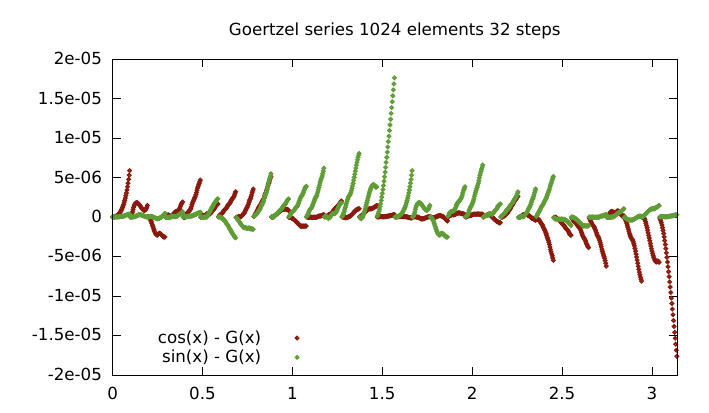
Goertzel's Algorithm

There are other ways to calculate series of sincos values quickly. One is Goertzel's Algorithm. It can calculate a series of sin/cos values of the form sincos(a + i*b), which is exactly what is required.

An example implementation:

 float cb = 2 * cos(b);
 // offset by 3 terms back
 float ag = a - 3 * b;

 // can be calculated using summation rule
 float s1 = sin(ga+b);
 float s0 = sin(ga+2*b);
 float c1 = cos(ga+b);
 float c0 = cos(ga+2*b);

 // unroll the inner loop once to simplify register usage/reusage
 for (int i=0;i<N;i+=2) {
    s1 = cb * s0 - s1;
    c1 = cb * c0 - c1;
    s0 = cb * s1 - s0;
    c0 = cb * c1 - c0;

    out[i+0] = c1 + s1 * I;
    out[i+1] = c0 + s0 * I;
 }

Unfortunately, floating point addition pretty much sucks so this will drift very quickly if cb*X is appreciably different in scale to Y in the cb*x-Y expressions. So error depend on both b and a, which leads to a funky looking error plot.

Where a = j*32*PI/1024 | j= (0 ... 31), b = PI/1024.

Was worth a try I guess.

asm v c

For a bit of 'fun' i thought i'd see how translating some of the fft code to assembly would fare.

I started with this:

void
build_wtable(complex float *wtable, int logN, int logStride, int logStep, int w0) {
        int wcount = 1<<(logN - logStep - 2);
        int wshift = logStride;

        for (int i=0;i<wcount;i++) {
                int j0 = w0 + (i<<wshift);
                int f2 = j0 << (CEXPI_LOG2_PI - logN + logStep - logStride + 1);
                int f0 = f2 * 2;

                wtable[i*2+0] = ez_cexpii(f0);
                wtable[i*2+1] = ez_cexpii(f2);
        }
}

It generates the twiddle factors required for a given fft size relative to the size of the data. ez_cexpii(x) calculates e^(I * x * PI / (2^20)), as previously discussed.

This is called for each radix-4 pass - 5 times per 1024 elements, and generates 1, 4, 16, 64, or 256 complex value pairs per call. I'm timing all of these together below so this is the total time required for twiddle factor calculation for a 1024-element FFT in terms of the timer counter register.

The results:

                what  clock    ialu    fpu   dual  e1 st  ra st  loc fe  ex ld  size
                noop     23       4      0      0      9     16      8      6
        build_wtable  55109   36990   9548   6478      9   7858      1      6    372
     build_wtable_il  62057   25332   9548   4092      9  27977      8      6    618
      e_build_wtable  31252   21999   9548   8866      9   7518     13      6    464
   e_build_wtable_hw  29627   21337   9548   8866     24   7563     16     36    472

  1 * e_build_wtable    148      99     28     26      9     38      1      6

$ e-gcc --version
e-gcc (Epiphany toolchain (built 20130910)) 4.8.2 20130729 (prerelease)

(30 000 cycles is 50uS for a clock of 600Mhz)

noop

This just calls ez_timer0_start(timerid, ~0); ez_ctimer0_stop(); and then tallies up the counters showing a baseline for a single time operation.

build_wtable

This is the code as in the fft sample.

build_wtable_il

This is the same as above but the ez_cexpii() call has been inlined by the compiler.

e_build_wtable

The assembly version. This is after a few hours of poking at the code trying to optimise it further.

e_build_wtable_hw

The same, but utilising the hardware loop function of the epiphany.

Discussion

Well what can i say, compiler loses again.

I'm mostly surprised that inlining the cexpii() function doesn't help at all - it just hinders. I confirmed the code is being inlined from the assembler listing but it just seems to be more or less copying the code in-lined twice rather than trying to interleave the functions to provide additional scheduling opportunities. As can be seen the ialu ops are significantly reduced because the constant loads are being taken outside of the loop but that is offset by a decrease in dual-issue and a big jump in register stalls.

Whilst the compiler generated a branch in the cexpii function I managed to go branchless in assembly by using movCC a couple of times. I am loading all the constants from a memory table using ldr which reduces the ialu op count a good bit, although that is outside the inner loop.

The hardware loop feature knocks a little bit off the time but the loop is fairly large so it isn't really much. I had to tweak the code a little to ensure the code lined up correctly in memory otherwise the loop got slower. i.e. such that .balignw 8,0x01a2 did nothing although it is still present to ensure correct operation.

Try as I might I was unable to get every flop to dual issue with an in ialu op. Although I got 26 out of 28 to dual-issue which seems ok(?). I don't fully understand the interaction of the dual-issue with things like instruction order and alignment so it was mostly just trial and error. Sometimes moving an instruction which had no other dependency could change the timing by a bigger jump than it should have, or e.g. add one ialu instruction and now the total clock time is 3 clock cycles longer?

I'm not sure I understand the register stall column completely either. For example calling the function such that a single result pair is calculated results in the last row of the table above. 38 stalls, where? The noop case is easier to analyse in detail: where do those 16 stalls come from? AFAICT the instruction sequence executed is literally:

  32:   3feb 0ff2       mov r1,0xffff
  36:   3feb 1ff2       movt r1,0xffff
  3a:   10e2            mov r0,r4
  3c:   1d5f 0402       jalr r15

-> calls 00000908 <_ez_ctimer0_start>:

 908:   6112            movfs r3,config
 90a:   41eb 0ff2       mov r2,0xff0f
 90e:   5feb 1ff2       movt r2,0xffff
 912:   4d5a            and r2,r3,r2
 914:   4102            movts config,r2
 916:   390f 0402       movts ctimer0,r1
 91a:   0096            lsl r0,r0,0x4
 91c:   487a            orr r2,r2,r0
 91e:   4102            movts config,r2

-> clock starts counting NOW!

 920:   194f 0402       rts

-> returns to timing loop:

  40:   0112            movfs r0,config
  42:   02da            and r0,r0,r5
  44:   0102            movts config,r0

-> clock stops counting NOW!

  46:   391f 0402       movfs r1,ctimer0
  4a:   1113            add r0,r4,2
  4c:   270a            eor r1,r1,r6
  4e:   0056            lsl r0,r0,0x2

etc.

Attempting to analyse this:

4 ialu - integer alu operations

Yep, 4 instructions are executed.

6 ex ld - external load stalls

This is from reading the config register.

8 loc fe - local fetch stalls

From the rts switching control flow back to the caller?

16 ra st - register dependency stalls

Considering no registers are being directly accessed in this section it's a little weird. rts will access lr (link register) but that shouldn't stall. The instruction fetch will access the PC, not sure why this would stall.

Still puzzled. 23 clock cycles for { rts, movfs, and, movts }, apparently.

parallella ezesdk 0.3(.1)

Just uploaded another ezesdk snapshot as ezesdk 0.3 to it's home page.

Didn't do much checking but it has all the recent stuff i've been playing with from auto-resource referencing to the fft code.

Update: Obviously didn't do enough checking, the fft sample was broken. I just uploaded 0.3.1 to replace it.

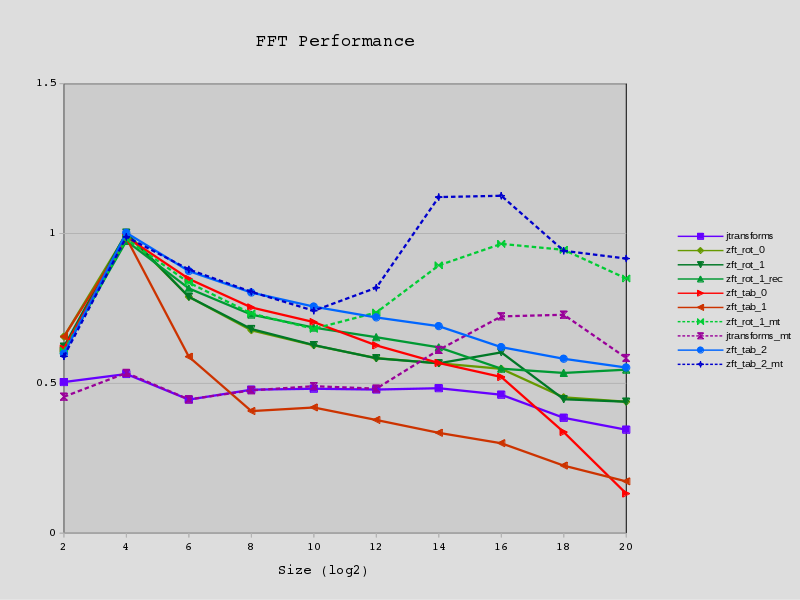
FFT(N=2^20) parallella/epiphany, preliminary results

I finally (finally) got the fft routine running on the epiphany. It's been a bit of a journey mostly because each time I made a change I broke something and some of the logarithmic maths is a bit fiddly and I kept trying to do it in my head. And then of course was the days-long sojourn into calculating sine and cosine and other low-level issues. I just hope the base implementation I started with (radix-2) was correct.

At this point i'm doing synchronous DMA for the transfers and I think the memory performance is perhaps a little bit better than I thought from a previous post about bandwidth. But the numbers still suggest the epiphany is a bit of an fpu monster which has an impedance mismatch to the memory subsystem.

The code is under 2.5K in total and i've placed the code and stack into the first bank with 3 banks remaining for data and twiddle factors.

First the timing results (all times in seconds):

 rows columns noop    fft     ffts   radix-2

   1    1     0.234   0.600
   2    1             0.379
   1    2             0.353
   4    1     0.195   0.302
   1    4     0.233   0.276
   2    2     0.189   0.246
   4    4     0.188   0.214
  arm         -       1.32    0.293   2.17

The test is a single out-of-place FFT of 2^20 elements of complex float values. The arm results are for a single core.

noop

This just performs the memory transfers but does no work on the data.

fft

The fft is performed on the data using two passes of a radix-1024 step. The radix-1024 step is implemented as 5 passes of radix-4 calculations. Twiddle factors are calculated on-core for each radix-4 pass.

The first outer pass takes every 1024th element of input, performs a 1024 element FFT on it, and then writes it back sequentially to memory (out-of-place).

The second outer pass takes every 1024th element, performs a 1024 element FFT on it but with a phase shift of 1/(2^20), and then writes it back to the same memory location they came from (in-place).

ffts

Using the Fastest Fourier Transform in the South on an ARM core. This is a code-generator that generates a NEON optimised plan.

radix-2

A out-of-place radix-2 implementation which uses a pre-calculated lookup-table for the sin/cos tables. The lookup-table calculation is not included but it takes longer than the FFT itself.

Discussion

Firstly, it's a bit quicker than I thought it would be. I guess my previous DMA timing tests were out a little bit last time I looked or were broken in some way. The arm results (outside of ffts) are for implementations which have particularly poor memory access patterns which explains the low performance - they are pretty close to worst-case for the ARM data cache.

However as expected the limiting factor is memory bandwidth. Even with simple synchronous DMA transfers diminishing returns are apparent after 2 active cores and beyond 4 cores is pointless. Without the memory transfers the calculation is around 10x faster in the 16-core case which shows how much memory speed is limiting performance.

Compared to complexity of ffts (it was the work of a PhD) the performance isn't too bad. It is executing a good few more flops too because it is calculating the twiddle factors on the fly. 1 396 736 sin/cos pairs are calculated in total.

Further stuff

I've yet to try asynchronous DMA for interleaving flops and mops. Although this would just allow even fewer cores to saturate the memory bus.

Currently it runs out-of-place, which requires 2x8MB buffers for operation. I can't see a way to re-arrange this to become in-place because of the butterfly of the data required between the two outer passes.

The memory transfers aren't ideal for the parallella. Only the write from the first pass is a sequential DMA which increases the write bandwidth. The only thing I can think of here is to group the writes across the epiphany chip so at least some of the writes can be in sequential blocks but this would add complication and overheads.

The inner loops could be optimised further. Unrolling to help with scheduling, assembly versions with hardware loops, or using higher radix steps.

The output of the last stage is written to a buffer which is then written using DMA, it also requires a new pair of twiddle factors calculated for each step of the calculation which passes through an auxiliary table. These calculations could be in-lined and the output written directly to the external memory (although the C compiler only uses 32-bit writes so it would require assembly language).

The code is hard-coded to this size but could be made general purpose.

The implementation is small enough it leaves room for further on-core processing which could help alleviate the bandwidth issue (e.g. convolution).

It should be possible to perform a radix-2048 step with the available memory on-core which would raise the upper limit of a two-pass solution to 2^22 elements, but this would not allow the use of double-buffering.

I haven't implemented an inverse transform.

static resource init

I noticed some activity on a thread in the parallella forum and whilst following that up I had another look at how to get the file loader to automgically map symbols across multiple cores.

Right now the loader will simply resolve the address to a core-local address and the on-core code needs to manually do any resolution to remote cores using ez_global_address() and related functions.

First I tried creating runtime meta-data for symbols which let the loader know how the address should be mapped on a given core. Once I settled on some basic requirements I started coding something up but quickly realised that it was going to take quite a bit of work. The first approach was to use address matching so that for example any address which matched a remapped address could be rewritten as necessary. But this wont work because in-struct addresses could fall through. So then I thought about using the reloc record symbol index. This could work fine if the address is in the same program on a different core, but it falls over if the label is in a different program; which is the primary case i'm interested in. Then I looked into just including a symbolic name but this is a bit of a pain because the loader then needs to link the string pointers before it can be used. So I just copied the symbol name into a fixed sized buffer. But after all that I threw it away as there were still a couple of fiddly cases to handle and it just seemed like too much effort.

So then I investigated an earlier idea I had which was to include some meta-data in a mangled symbol name. One reason I never followed it up was it seemed too inconvenient but then I realised I could use some macros to do some of the work:

  #define REF(var, row, col) _$_ ## row ## $_ ## col ## $_ ## var

  // define variable a stored on core 0,0
  extern int REF(a, 0, 0);

  // access variable a on core 0,0
  int b = REF(a, 0, 0);

This just creates a variable named "_$_0$_0$_a" and when the loader goes to resolve this symbol it can be mapped to the variable 'a' on the specific core as requested (i'm using _N to map group-relative, or N to map this-core-relative). The same mechanism just works directly for symbols defined in the same program as well since the linker doesn't know of any relation between the symbols.

So although this looked relatively straightforward and would probably work ... it would mean that the loader would need to explicitly relink (at least some of) the code for each core at load-time rather than just linking each program once and copying it over as a block; adding a lot of on-host overheads which can't be discounted. It didn't really seem to make much difference to code size in some simple tests either.

So that idea went out the window as well. I think i'll just stick to hand coding this stuff for now.

resources

However I thought i would revisit the meta-data section idea but use it in a higher level way: to define resources which need to be initialised before the code executes - e.g. to avoid race conditions or other messy setup issues.

I coded something up and it seems to be fairly clean and lean; I might keep this in. It still needs a bit of manipulation of the core image before it gets copied to each core but the processing is easier to separate and shouldn't have much overhead.

An example is initialising a port pair as used in the workgroup-test sample. There is actually no race condition here because each end only needs to initialise itself but needing two separate steps is error prone.

First the local endpoint is defined with a static initialiser and then it's reference to the remote port is setup at the beginning of main.

extern ez_port_t portb EZ_REMOTE;

ez_port_t porta = {
  .mask = 4-1
};

main() {
    int lid = ez_get_core_row();

    ez_port_setup(&aport, ez_global_core(&bport, lid, 0));

   ... can now use the port
}

This sets up one end of a port-pair between two columns of cores. Each column is loading a different program which communicates with the other via a port and some variables.

Using a resource record, this can be rewritten as:

extern ez_port_t bport EZ_REMOTE;

// includes the remote port which the loader/linker will resolve to the
// lower 15 bits of the address
ez_port_t aport = {
    .other = &bport,
    .mask = 4-1
};

// resource record goes into .eze.restab section which is used but not loaded
// the row coordinate is relative, i.e. 'this.row + 0',
// and the column of the target is absolute '1'.
static const struct ez_restab __r_aport
__attribute__((used,section(".eze.restab,\"\",@progbits ;"))) = {
    .flags = EZ_RES_REL_ROW | EZ_RES_PORT,
    .row = 0,
    .col = 1,
    .target= &aport
};

main() {
    ... can now use the port
}

It looks a bit bulky but it can be hidden in a single macro. I guess it could also update an arbitrary pointer too and this isn't far off what I started with - but it can only update data pointers not in-code immediate pointer loads that elf reloc records allow for.

Not sure what other resources I might want to add though and it's probably not worth it for this alone.

cexpi, power of 2 pi

I did a bit more playing with the sincos stuff and ended up rolling my own using a taylor series.

I was having issues with using single floating point to calculate the sincos values, the small rounding errors add up over a 1M element FFT. I tried creating a fixed-point implementation using 8.24 fixed point but that was slightly worse than a float version. It was quite close in accuracy though, but as it requires a 16x32-bit multiply with a 48-bit result, it isn't of any use on epiphany. For the integer algorithm I scaled the input by 0.5/PI which allows the taylor series coefficients to be represented in 8.24 fixed-point without much 'bit wastage'.

My final implementation uses an integer argument rather than a floating point argument which makes it easier to calculate the quadrant the value falls into and also reduces rounding error across the full input range. It calculates the value slightly differently and mirrors the angle in integer space before converting to float to ensure no extra error is added - this and the forming of the input value using an integer is where the additional accuracy comes from.

I tried a bunch of different ways to handle the swapping and ordering of the code (which surprisingly affects the compiler output) but the following was the best case with the epiphany compiler.

/*
 Calculates cexp(I * x * M_PI / (2^20))
   = cos(y) + I * sin(y)  |y = (x * M_PI / (2^20))

  where x is a positive integer.

  The constant terms are encoded into the taylor series coefficients.
*/
complex float
ez_cexpii(int ai) {
    // PI = 1
    const float As = 3.1415926535897931159979634685441851615906e+00f;
    const float Bs = -5.1677127800499702559022807690780609846115e+00f;
    const float Cs = 2.5501640398773455231662410369608551263809e+00f;
    const float Ds = -5.9926452932079210533800051052821800112724e-01f;
    const float Es = 8.2145886611128232646095170821354258805513e-02f;
    const float Fs = -7.3704309457143504444309733969475928461179e-03f;

    const float Bc = -4.9348022005446789961524700629524886608124e+00f;
    const float Cc = 4.0587121264167684842050221050158143043518e+00f;
    const float Dc = -1.3352627688545894990568285720655694603920e+00f;
    const float Ec = 2.3533063035889320580018591044790809974074e-01f;
    const float Fc = -2.5806891390014061182789362192124826833606e-02f;

    int j = ai >> (20-2);
    int x = ai & ((1<<(20-2))-1);

    // odd quadrant, angle = PI/4 - angle
    if (j & 1)
        x = (1<<(20-2)) - x;

    float a = zfloat(x) * (1.0f / (1<&lt20));
    float b = a * a;

    float ssin = a * ( As + b * ( Bs + b * (Cs + b * (Ds + b * (Es + b * Fs)))));
    float scos = 1.0f + b * (Bc + b * (Cc + b * (Dc + b * (Ec + b * Fc))));

    int swap = (j + 1) & 2;

    if (swap)
        return bnegate(ssin, j+2, 2) + I * bnegate(scos, j, 2);
    else
        return bnegate(scos, j+2, 2) + I * bnegate(ssin, j, 2);
}

This takes about 90 cycles per call and provides slightly better accuracy than libc's sinf and cosf (compared on amd64) across the full 2PI range. The function is 242 bytes long. If the taylor series only used 5 terms is about as accurate as libc's sinf and cosf and executes 6 cycles faster and fits in only 218 bytes.

Apart from accuracy the other reason for having a power of 2 being PI is that this what is required for the FFT anyway so it simplifies the angle calculation for that.

Whether this is worth it depends on how long it would take to load the values from a 1M entry table

As per the previous post a radix-1024 fft pass (using radix-4 fft stages) requires 341 x 2 = 682 sincos pairs for one calculation. For the first pass this can be re-used for each batch but for the second values must be calculated (or loaded) each time. This is approximately 61K cycles.

The calculation of the radix-1024 pass using radix-4 stages itself needs 1024 / 4 x log4(1024) x 8 complex multiply+add operations, or at least 40K cycles (complex multiply+add using 4xfma) plus some overheads.

Going on the memory profiling i've done so far, it's probably going to be faster calculating the coefficients on-core rather than loading them from memory and saves all that memory too.

sincos

So i've continuted to hack away on a 1M-element fft implementation for epiphany.

The implementation does 2xradix-1024 passes. The first just does 1024x1024-element fft's, and the second does the same but on elements which are strided by 1024 and changes the twiddle factors to account for the frequency changes. This lets it implement all the reads/writes using LDS and it only has to go to global memory twice.

At this point i'm pretty much doing it just for something to do because I did some testing with ffts and that can execute on a single arm core about 2x faster than the epiphany can even read and write the memory twice because all global memory accesses are uncached. According to some benchmarks I ran anyway - assuming the rev0 board is the same. Given that it's about the same speed for accessing the shared memory in the same way from the ARM (it's non-cached) I think the benchmark was valid enough.

Anyway one problem is that it still needs to load the twiddle factors from memory and for the second pass each stage needs it's own set. i.e. more bandwidth consumption. Since there's such a flop v mop impedance mismatch I had a look into generating the twiddle factors on the epiphany core itself.

Two issues arise: generating the frequency offset, and then taking the cosine and sine of this.

The frequency offset involves a floating-point division by a power of two. This could be implemented using fixed-point, pre-calculating the value on the ARM (or at compile time), or a reciprocal. Actually there's one other way - just shift the exponent on the IEEE representation of the floating point value directly. libc has a function for it called scalbnf() but because it has to be standards compliant and handle edge cases and overflows it's pretty bulky. A smaller/simpler version:

float scalbnf(float f, int logN) {
    union {
        float f;
        int i;
    } u;

    u.f = f;
    if (u.i)
        u.i += (logN << 23);

    return u.f;
}

This shifts f by logN - i.e. multiplies f by 2^N, and allows division by using negative logN. i.e. divide by 1024 by using logN=-10.

The second part is the sine and cosine. In software this is typically computed using enough steps of a Taylor Series to exhaust the floating point precision. I took the version from cephes which does this also but has some pre-processing to increase accuracy with fewer steps; it's calculation only works over over PI/4 and it uses pre and post-processing to map the input angle to this range.

But even then it was a bit bulky - standards compliance/range checking and the fpu mode register adds a bit of code to most simple operations due to hardware limitations. Some of the calculation is shared by sin and cos, and actually they both include the same two expressions which get executed depending on the octant of the input. By combining the two, removing the error handling, replacing some basic flops with custom ones good enough for the limited range and a couple of other tweaks I managed to get a single sincosf() function down to 222 bytes verses 482 for just the sinf() function (it only takes positive angles and does no error checking on range). I tried an even more cut-down version that only worked over a valid range of [0,PI/4] but it was too limited to be very useful for my purposes and it would just meant moving the octant handling to another place so wouldn't have saved any code-space.

I replaced int i = (int)f with a custom truncate function because I know the input is positive. It's a bit of a bummer that FIX changes it's behaviour based on a config register - which takes a long time to modify and restore.

I replaced float f = (float)i with a custom float function because I know the input is valid and in-range.

I replaced most of the octant-based decision making with non-branching arithmetic. For example this is part of the sinf() function which makes sign and pre-processing decisions based on the input octant.

    j = FOPI * x; /* integer part of x/(PI/4) */
    y = j;
    /* map zeros to origin */
    if( j & 1 ) {
        j += 1;
        y += 1.0f;
    }
    j &= 7; /* octant modulo 360 degrees */
    /* reflect in x axis */
    if( j > 3 ) {
        sign = -sign;
        j -= 4;
    }

 ... calculation ...

    if( (j==1) || (j==2) ) {
      // use the sin polynomial
    } else {
      // use the cos polynomial
    }

    if(sign < 0)
        y = -y;
    return( y);

This became:

   j = ztrunc(FOPI * x);
   j += (j & 1);
   y = zfloat(j);
   sign = zbnegate(1.0f, j+1, 2);
   swap = (j+1) & 2;

 ... calculation ...
    if( swap ) {
      // use the sin polynomial
    } else {
      // use the cos polynomial
    }

    return y * sign;

Another function zbnegate negates it's floating point argument if a specific bit of the input value is set. This can be implemented straightforward in C and ends up as three CPU instructions.

static inline float zbnegate(float a, unsigned int x, unsigned int bit) {
    union {
        float f;
        int i;
    } u;

    u.f = a;
    u.i ^= (x >> bit) << 31;

    return u.f;
}

Haven't done any timing on the chip yet. Even though the original implementation uses constants from the .data section the compiler has converted all the constant loads into literal loads. At first I thought this wasn't really ideal because double-word loads could load the constants from memory in fewer ops but once the code is sequenced there are a lot of execution slots left to fill between the dependent flops and so this ends up scheduling better (otoh such an implementation may be able to sqeeze a few more bytes out of the code).

Each radix-1024 fft needs to calculate 341x2 sin/cos pairs which will add to the processing time but the number of flops should account for the bandwidth limitations and it saves having to keep it around in memory - particularly if the problem gets any larger. The first pass only needs to calculate it once for all batches but the second pass needs to calculate each individually due to the phase shift of each pass. Some trigonometric identities should allow for some of the calculations to be removed too.

borkenmacs

Emacs is giving me the shits today. It always used to be rock-solid but over the last few years the maintainers have been breaking shit left right and centre.

• Indenting is slower than it used to be (and it was already pretty slow) and keeps breaking all the time - I have to keep quitting a file when it decides it's lost the plot and reload it;
• Some fool thought that a line-oriented text-editor should track the cursor by visual lines by default;
• c-macro-expand comes broken as packaged with a useless error message whenever you run it (incorrect cpp definition);
• Locally rendered text bitmaps. i.e. slow text rendering, and slow as all shit over remote X11. And no misc-fixed fonts unless you hunt for them - i.e. shit fonts;
• Shitty menu's and a really pointless toolbar that need to be turned off. The toolbar often breaks focus if it's left on;
• Crappy colours, but then again most GNU/linux tools suffer from that and it's probably more to do with distro wank.

Some of it can be fixed by local configuration, but the rest is probably best fixed by going back to a previous version and compiling without the gtk+ toolkit.

Update: Oh i almost forgot because I haven't seen it in a while, bloody undo got broken at some point. It's particularly broken on ubuntu for some reason (where I just saw it, I don't normally use ubuntu but that's what parallella uses). Sometimes editing a file you can only undo a few lines. This is particularly bad if it's in the middle of a kill-yank-undo cycle as you can end up with unrecoverably lost work.

For a text editor I can think of no higher sin.