About Me
Michael Zucchi
B.E. (Comp. Sys. Eng.)
also known as Zed
to his mates & enemies!
< notzed at gmail >
< fosstodon.org/@notzed >

post weekend
I did a bit more work on the ezetool code - most improvements to the output. Added labels, each function has the cycle counters reset, and branch targets are calculated.
As a bit of an experiment I wrote a tiny bit of a simulator - just enough to simulate all the instructions in isqrt().
Simulation of calculating an approximation to iqsrt(9) (i.e. 1/3):
000000: mov.l r2,#0x0000 r2 <- 00000000 0.000000
000004: movt.l r2,#0x3f00 r2 <- 3f000000 0.500000
000008: mov.l r1,#0x59df r1 <- 000059df 0.000000
00000c: fmul.s r2,r0,r2 r2 <- 40900000 4.500000
00000e: movt.l r1,#0x5f37 r1 <- 5f3759df 13211836172961055000.000000
000012: asr.s r0,r0,#0x0001 r0 <- 20880000 41100000
000014: sub.s r0,r1,r0 r0 <- 3eaf59df
000016: mov.l r1,#0x0000 r1 <- 00000000 0.000000
00001a: movt.l r1,#0x3fc0 r1 <- 3fc00000 1.500000
00001e: fmul.s r2,r2,r0 r2 <- 3fc5451b 1.541171
000020: fmsub.s r1,r2,r0 r1 <- 3f78e082 0.972176
000022: fmul.s r0,r1,r0 r0 <- 3eaa78d8 0.332953
000024: jr.l r14
But it was just using the string names of the instructions in a switch statement and was a bit bulky so I started looking into ways of making it easier to write and ended up falling down a pretty deep rabbit hole before I decided I don't really want to write a simulator anyway (well, probably not).
One thing I was looking at was including the instruction operation in the instruction definition file directly, so i started playing with an expression parser. I came up with a pretty novel (or perhaps, just shit) non-recursive parser implemented using a hand-coded state machine and a few stacks but it wasn't anything more than a bit of piss farting about.
But this playing with an expression parser got me thinking about a programmers calculator. I mostly fire up a random xterm and run gdb whenever I want to do some sort of calculation (going by ps i currently have 9 littered across 4 virtual desktops amongst 38 xterms and 8 copies of emacs) but although that serves most of my needs very well sometimes it just doesn't. Sometimes I need to write little C or java snippets or resort to an old Sharp calculator.
Today mostly out of curiosity I had a look at some compiler generator tools - i found that bison has a Java output which although it doesn't seem to be actively developed appears to function ok. I started with my own lexical analyser but that quickly got messy so I tried jflex which did the job fine. These are the sort of tools I play with out of curiosity every few years but never do anything useful with - i think they're kinda nifty but never seem to have a real need for them.
gdb also has has a command line. Thus deeper down the rabbit hole I went looking for a readline equivalent for Java. I looked at one but it had a few external dependencies and uses maven to resolve them (which means: just no). So ... I mucked about for a couple of hours writing my own. Using stty to set the terminal to raw mode and then creating a stream which decodes the escape sequences. Of course I've forgotten everything i did with zvt (gnome-terminal 1.0) but it didn't take long to get a single-line editor going with basic functions like navigation, editing, and history. But probably it may as well just have it's own window so that was mostly just a bit of pointless mucking about and I probably should've just been playing with doing it with a gui toolkit.
Then the weekend ended.
I dunno, maybe I'll keep playing around with it, or maybe I wont.
At least I finally pruned the roses and re-trained some of them onto stakes. Kinda been letting them go a bit. Did a bit of other gardening stuff too - it turned out to be an ok enough day with a bit of sunshine and a little warmth although it didn't last long.
instruction matching
This was an interesting little diversion.
One of the requirements of a disassembler or code translator is to work out from the machine code what instruction is at a given address. Most instruction sets are variable in size so it has to determine that as well.
Depending on how the instruction set was designed this can either be a simple table lookup, ... or get somewhat more involved. It usually can't just be all a simple lookup though as there are usually some instructions that want to use most of the bits for data.
Linear
The current implementation in ezetool uses a simple linear search. For each instruction it sees if all the selector bits for the instruction match the test bits. This is trivial:
boolean match = (select_mask & opcode) == select_bits;
It has to be executed up to two times because it doesn't know the instruction size yet. Bit 3 has that information for many instructions but not all.
Linear split
An obvious improvement that I didn't have time for initially is to split the search into two separate lists. One for 16-bit instructions and one for 32-bit instructions. Because it just Has To Be, all 32-bit instructions will be different in their first 16-bits to all 16-bit instructions so the lists can be separated.
This amounts to a pre-indexing of the instructions based on their size and lead to over 100% performance increase.
List of Hash Tables
A hashtable can't be used directly because you don't know in advance which of the bits are significant.
This can be shown by displaying the instructions which use the same selector bits as i'm using them. Some of the 'selector' bits here are separating instructions into different addressing modes which could be handled in a different way (the high-bits of the ldr and mov instructions) but this is the way i've written it so far.
0000000f: b b (16/32 bit variants)
0000001f: ldr str ldr str ldr str mov lsr lsl asr bitr
0000007f: add sub add sub add sub and orr eor asr lsr lsl fadd fsub fmul fmadd fmsub
0000030f: mov
000003ff: float fix fabs movts movfs jr jalr gie gid nop idle bkpt mkpt sync rti wand trap
000f001f: lsr lsl asr bitr
000f007f: add sub and orr eor asr lsr lsl fadd fsub fmul fmadd fmsub
000f030f: mov
000f03ff: float fix fabs movts movfs jr jalr
0200001f: ldr str ldr str
0060001f: ldr str testset ldr str
1000001f: mov movt
A solution here would perform a linear search across all select-bit combinations, and each of those would be accessed via a hash table. Given the simplicity of the comparison test though it may as well just be a linear search.
I didn't try implementing this but as it removes the smask de-reference outside of the inner loop it may be ok.
Radix/index M-tree
Looking at the output above it is clear that at least 0x0f is used as a selector bit in every instruction. This can be used to create a first-level index and reduce the search space.
Indexing by the first nybble:
0 [ 1]: b
1 [ 2]: ldr str
2 [15]: mov movts movfs jr jalr gie gid nop idle bkpt mkpt sync rti wand trap
3 [ 3]: mov add sub
4 [ 2]: ldr str
5 [ 2]: ldr str
6 [ 2]: lsr lsl
7 [ 8]: fadd fsub fmul fmadd fmsub float fix fabs
8 [ 1]: b
9 [ 3]: ldr str testset
a [ 8]: add sub and orr eor asr lsr lsl
b [ 4]: mov movt add sub
c [ 4]: ldr str ldr str
d [ 2]: ldr str
e [ 2]: asr bitr
f [25]: lsr lsl asr bitr add sub and orr eor asr lsr lsl fadd fsub fmul fmadd
fmsub float fix fabs mov movts movfs jr jalr
Well, it's simple ... but not very effective.
I did some analysis of the longer sets above and found most instructions use either 0x70 or 0xf0 as selector bits so a further level of m-tree can be added for those. For the others I just dump them into a linear search.
This reduces the worst-case to:
f: lsr lsl asr bitr mov
0: eor fadd movts
1: add fsub movfs
2: lsl fmul
3: sub fmadd
4: lsr fmsub jr
5: and float jalr
6: asr fix
7: orr fabs
Which involves: a direct radix-index based on the first 4 bits, a 2 or 3 element linear search from a 3-bit radix, and a 5-element linear search across the 'leftovers'. This turned out to be very fast - about 6x faster than the linear search, but did require a bit of human input for the tree sizes.
Radix/sparse tree
I'm not really sure what to call this but i guess its a sort of radix search but with a sparse tree. I was seeing if i could fully automate the tree building.
Each significant bit is indexed from the lsb upwards. Each tree node has a list of child nodes which specify which bit and bit-value they correspond to. The first 4 levels of the tree are fully filled but as the selector bits change it becomes a sparse tree.
My initial naive thought was that this could find a solution in one pass like a huffman code but of course this isn't the case: it still has to perform a fairly wide search because, again, it doesn't know which bits are significant (if it did, then it would work in one pass).
I implemented this as a 4-bit radix (i.e. index) into 16 separate trees. It was faster than a linear search but not as fast as the split-linear. I didn't think it was worth the effort to try to optimise the tree so that it would resemble the indexed m-tree.
8-bit index
So at this point I had a pretty good/quick implementation but wondered if i could get any better.
I tried using 8 bits for the first-stage index rather than 4. This complicates matters a little bit because many (most?) instructions don't use the first 8-bits as a selector which means they will alias to multiple locations. The solution: just alias them. So for example 'b' uses only 4 bits as a selector so one ends up with 16 copies.
Here's a part of the table.
0: b
1: ldr
2: mov movts
3: mov
4: ldr
5: ldr
6: lsr
7: fadd
8: b
9: ldr testset
10: eor
11: mov movt
12: ldr ldr
13: ldr
14: asr
15: lsr asr eor fadd mov movts
The worst case (over the whole table) is a single 8-bit indexed lookup followed by 6-element linear search.
Simple code, needs moderate space, and runs really fast ... well most of the time. At least in Java it has some strange cache-related effects so depending on the memory layout its runtime varies by nearly 100%.
Since most instructions don't use all 8-bits as a selector i also tried using 7 or 6 bits. For 7 bits the maximum run is still 6: i.e. well wasn't using 8 silly but with the half the index size. For 6-bits a couple of the runs got slightly longer but it takes half of the index size again.
Micro-Optimisations
I also looked at a bunch of micro-optimisations to the data-structures.
For the linear search, rather than iterating through a list of objects which require a dereference, iterate through a single array of integers which contain the selector mask and bits together. This could be applied anywhere a linear search is although other cases also need to include the instruction index.
Very slight improvement - Java seems good at object dereferences but it might be applicable to c.
I also tried flattening one of the array of lists implementations into a single list of integers. The first N elements are just indices into the array and then the structure at each array is a count followed by { mask, value, index } triplets. Well Java didn't really like this so it wasn't an improvement.
Numbers
I realised all implementations require two lookups so I did timed that. I didn't bother timing the ones which weren't competitive for a single lookup pass.
This is for 100 000 iterations of looking up every instruction in order (84 using my splits). So even the slowest implementation is only 120ns 18ns in Java on a Kaveri CPU. In all cases any lists required during building were collapsed to arrays of exactly the right size - arrays are much smaller than lists and iterate faster.
time memory alg
1.013 0 linear search
0.449 2 linear split search
0.157 (2+64*2)*2+84 344 0x3f index + linear search
0.153 (2+128*2)*2+84 600 0x7f index + linear search
0.180 6*(2+6)+72+84 204 multi-stage radix + linear search
The memory is the approximate extra words required to store the indices. An array is counted as 2 words + space for the contents (length+pointer+data). The multi-stage thing needs the bit number/mask and two arrays and I might have an error there.
Based on that I would probably go with the 0x3f indexed version. The building of the indices is easier than the multi-stage radix algorithm and it doesn't require an additional object (it just uses a 2d array) and memory requirements are modest compared to the 0x7f version with much the same runtime.
Still, it's only about 2.8x faster which is surprising given that the search is an order of magnitude less work, between 0 and 9 linear steps compared to 84 (or on average 4.5 vs 42). The benchmark is probably just not a good one.
Addendum
So there is a very cheap way to determine if the instruction is 16-bits or 32-bits. The first nybble is enough to determine this - i vaguely recall something like that but for some reason I thought it required a bigger table.
boolean isShortInstruction(int opcode) {
return ((0x44ff >> (opcode&0x0f)) & 1) == 1;
}
I added it and re-ran the benchmarks. It makes a measurable but pretty insignificant difference to the indexed implementations. The lookup is already fast enough that loop overheads and other scaffolding must be the dominating factor.
The linear search gained a lot because for a 32-bit instruction all 16-bit instructions had to be scanned before you could determine it wasn't one of them.
time memory alg
1.013 0 linear search (original)
0.296 2 split linear split search
0.156 (2+64*2)*2+84 344 split 0x3f index + linear search
0.149 (2+128*2)*2+84 600 split 0x7f index + linear search
TBH the linear search is fast for the purposes of a command-line tool but I rolled these improvements into the implementation anyway.
It's time ... it's time for some e-zed-e-time
I just uploaded the current state of the epiphany cpu instruction timing tool i've been working on.
It was supposed to be a super-quick chuck-together of what I had but I cleaned up the code and did a big re-factor (everything was in one namespace) and a bunch more. Toolification, building, packaging, readme, webpage, ... so this post will be short.
I haven't done much testing/verification beyond a few small test-cases, so bugs are a given.
It's on the ezetool (now with ezetime(tm)) home page, as is an example of the current outputs.
more tooling around
So i've done a bit more work on the tools and am getting pretty close to the first cut of the timing tool. I did some code tidying and created a separate disassembler tool.
I improved the disassembler output to include the machine code and symbols and handle all addressing modes properly. Yet to do is adding symbols for branch targets (or displaying branch target addresses) and showing aliases for the special registers.
01: 1 SHT_PROGBITS .text 00000000 00000038 000001a0 0 0 0 0000008 SHF_ALLOC SHF_EXECINSTR
_e_build_wtable:
0: 070094fc strd.l r4,[r13],#-1
4: 0400d47c strd.l r6,[r13,#+0]
8: 2002800b mov.l r12,#0x0000
c: a40090ec ldrd.l r44,[r12,#+1]
10: 8023 mov.s r4,#0x0001
12: a400d16c ldrd.l r46,[r12,#+2]
16: 400a312f lsl.l r17,r4,r2
1a: c40011ec ldrd.l r48,[r12,#+3]
1e: a5ba sub.s r5,r1,r3
20: c400526c ldrd.l r50,[r12,#+4]
Pipeline simulator
I did get the timing tool pretty close to functional but then the edge cases started getting messy and I tried reworking it a couple of times.
My current pipeline is something like this:
-> fetch [1] [0] instructions decoded into a 2-element queue
| |
decode and issue detect dual issue, assign pipeline
\ /
X cross-bar switch/router
/ \
DE DE implement RA stall logic. pair stalls together.
| |
RA RA implement E1 stall logic
| |
E1 E1 execute stages
| |
E2 E2
|
E3
|
E4
alu fpu alu = ialu, load/store, control
Note: This is a software-based model of the hardware so doesn't necessarily reflect the physical hardware; it just has to behave the same.
The pipeline is executed from the end backwards - serialising the inherently parallel process of a hardware pipeline but in a way which reaches the same result after each cycle. At each point an instruction only advances if the next pipeline slot is empty. Stalls can happen before RA or E1. I don't know if this is hardware-correct but the timings don't come out right otherwise.
At the fetch stage the next two instructions are read and decoded. Mainly this determines if each a 16-bit or 32-bit instruction and does some setup for the scheduling task. This approximates the way the hardware loads 8-byte instruction blocks and is required to implement the dual-issue logic. There are some fiddly details with the physical hardware that I haven't fully discovered yet (to do with instruction size, alignment, etc) but Andreas says it will probably change in future hardware and is not that important just yet.
The dual issue decision simply decides if both of the next instructions can be executed together. If they can they are then assigned to their respective pipelines and the fetch code is told to grab 2 new instructions. Dual issue rules are quite simple: no written register dependencies and one instruction must be an alu or load/store instruction and the other a floating point op. If they can't be dual-issued then only one instruction advances and the fetch code is told to get only one new one.
The next pipeline stage checks to see if the instructions have the registers they need. This is presumably meant to be in the 'RA' stage but if I put it there instructions are retired too early. If both pipelines contain an instruction (i.e. dual-issue) then they both must pass their register checks before either advance. To calculate if the registers are busy all the instructions present in all the other stages are scanned to determine what registers are still busy. There are some complications here because the answer depends on who's asking.
The next stage then checks for any registers read in E1. AFAIK this is only needed for the store instruction. Each pipeline is tested separately.
The instructions then pass through the pipeline stages until they retire.
My initial cut at the code had each instruction decide when it should reserve a register for itself and when it should mark the register as available (i.e. instruction completed). The decision was mostly based on addressing mode and the scheduling class (fpu/alu/load/control) with some hard-coded 'hacks' to handle specific variations like fmadd. This still wasn't enough as different instructions have different latencies depending upon which instruction is accessing it, and it also varies because some instructions can update two values. The code also tried to incrementally update the 'register busy' set but this was messy and error prone and multiple values needed to be maintained separately.
It got messy.
So i've been working on trying to convert it to a table-driven algorithm with fewer special cases.
After a few iterations this is some output from the current code:
code 0123456789abcdef0123456789abcdef0123456789abcdef0123456789abcdef
mov.l r1,#0x0000 | 1 |
nop.s | 1 |
ldr.s r0,[r1,#-0] | 123 |
fadd.s r0,r0,r0 | 1234 |
fadd.s r0,r0,r0 | 1234 |
str.s r0,[r1,#-0] | 1 |
The display needs a bit of tweaking but the execution start times and total running time of each instruction match what i'm getting out of the hardware counters (17 cycles total time).
The other output format I have shows the stalls are happening in the right place. There are 3 E1 stalls and 3+6 total register stalls which matches the hardware counters too. (It displays the alu ops continuing through the pipeline although most are retired after E1.)
DE RA E1 E2 DE RA E1 E2 E3 E4
alu: 0 mov - - - fpu: - - - - - -
alu: 1 nop 0 mov - - fpu: - - - - - -
alu: 2 ldr 1 nop 0 mov - fpu: - - - - - -
alu: - 2 ldr 1 nop 0 mov fpu: 3 fadd - - - - -
alu: - - 2 ldr 1 nop fpu: 3 fadd - - - - -
alu: - - - 2 ldr fpu: 3 fadd - - - - -
alu: - - - - fpu: 6 fadd 3 fadd - - - -
alu: - - - - fpu: 6 fadd - 3 fadd - - -
alu: - - - - fpu: 6 fadd - - 3 fadd - -
alu: - - - - fpu: 6 fadd - - - 3 fadd -
alu: - - - - fpu: 6 fadd - - - - 3 fadd
alu: 11 str - - - fpu: - 6 fadd - - - -
alu: 12 jr 11 str - - fpu: - - 6 fadd - - -
alu: 12 jr 11 str - - fpu: - - - 6 fadd - -
alu: 12 jr 11 str - - fpu: - - - - 6 fadd -
alu: 12 jr 11 str - - fpu: - - - - - 6 fadd
alu: 16 nop 12 jr 11 str - fpu: - - - - - -
alu: 17 b 16 nop 12 jr 11 str fpu: - - - - - -
alu: 18 b 17 b 16 nop 12 jr fpu: - - - - - -
I've annotated each instruction+addressing mode pair with a few pieces of information:
- srcRA
- Set of which registers rd,rn,rm are read by the instruction in RA
- srcE1
- Set of which registers rd,rn,rm are read by the instruction in E1, used by str instruction. I had to add a stall test in E1 to implement this.
- dALU, nALU
- How many cycles the d or n register is reserved in terms of alu instructions reading them. I've implemented this as a bit-mask but since every bit is set from 0-x it could just be a number.
- dFPU, nFPU
- How many cycles the d or nregister is reserved in terms of fpu instructions reading them.
Still a bit left like write-after-write stalls but I think that can use a similar mechanism. Things like double-loads or stores can be handled by seeing if the instruction has the appropriate size bits and using rd and rd+1. Because it's only a static analysis tool branches penalties and external loads are not required (although something for the latter might be nice, at least for special register access).
Time passes ... I added write-after-write stalls now (and double load/stores).
So, I think I now have enough guts; but I have go through a few tables and define correct values and then probably convert them into a resource file.
kettle + bucket
Hmm, no wonder my gas bill has always been high, and rising to stupid levels. Big gas leak :-/ Well plumber came, checked, turned it off. Given the volume of the leak i'm surprised I couldn't smell it more but it's underground in a steel pipe.
I've been thinking of getting solar hot water so maybe it's time to finally do that but I just don't want to have to sort anything out right now (i.e. my life; the story so far).
Perhaps cold showers will get me thinking faster. Although it's not bloody likely i'll have any of those; middle of winter and just washing your hands in cold water is ... well cold. Last time I had a hot-water problem was also in the middle of winter and it was an electric kettle and a bucket for a while (I was just about to sell the house and it needed a lot of renovation so getting it replaced wasn't worth it).
just bit of a tool
Weather turned south so I ended up hacking all afternoon again.
After posting the last article I went and had a look at the instruction decoder I was working on. First I was hand-coding it all but then I realised how silly it was so I put it into a simple table. I was going to make a code-generator from that but it's really not necessary.
Here's a tiny bit of the table (it's only 84 lines long anyway). It has 3 fields, instruction name, addressing mode, bit format.
; branches
b 7 i{7-0},c{3-0},v{0000}
b 7 i{23-0},c{3-0},v{1000}
; load/store
ldr 8 d{2-0},n{2-0},i{2-0},b{1-0},v{00100}
str 8 d{2-0},n{2-0},i{2-0},b{1-0},v{10100}
; alu
add 3 d{5-3},n{5-3},m{5-3},x{000},v{1010},d{2-0},n{2-0},m{2-0},v{0011111}
; etc.
The bit format just defines the bits in order as they are displayed in the instruction decode table, so were easy enough to enter.
From this table it's only about 10 lines of code to decode an instruction and not much more to display it - most of it is just handling the different addressing modes (ok it's a lot more but it's all a simple switch statement). It just searches for the instruction that matches all bits in the v{} sections; first in 16-bit instructions and if none are found then reads another 16 bits and looks in the 32-bit instructions. I still have some sign extension stuff to handle properly but here's some example output.
09: 1 SHT_PROGBITS .text.2
strd.l r4,[r13],#-2
strd.l r6,[r13,#+1]
strd.l r8,[r13,#+0]
mov.l r12,#0x0000
ldrd.l r44,[r12,#+0]
mov.s r4,#0x0001
ldrd.l r46,[r12,#+1]
lsl.l r17,r4,r2
ldrd.l r48,[r12,#+2]
sub.s r5,r1,r3
ldrd.l r50,[r12,#+3]
sub.s r6,r5,#0x0002
ldrd.l r52,[r12,#+4]
lsl.s r7,r4,r6
Here's the output from objdump for comparison.
Disassembly of section .text.2:
00000000 <_e_build_wtable2>:
0: 957c 0700 strd r4,[sp],-0x2
4: d4fc 0400 strd r6,[sp,+0x1]
8: 147c 2400 strd r8,[sp]
c: 800b 2002 mov r12,0x0
10: 906c a400 ldrd r44,[r12,+0x0]
14: 8023 mov r4,0x1
16: d0ec a400 ldrd r46,[r12,+0x1]
1a: 312f 400a lsl r17,r4,r2
1e: 116c c400 ldrd r48,[r12,+0x2]
22: a5ba sub r5,r1,r3
24: 51ec c400 ldrd r50,[r12,+0x3]
28: d533 sub r6,r5,2
2a: 926c c400 ldrd r52,[r12,+0x4]
2e: f32a lsl r7,r4,r6
Because I wrote this in Java, before I could even test it ... I had to write an elf library as well. But elf is simple so it was just a few 'struct' accessors for a memory mapped Java ByteBuffer and only took half an hour via some referencing of the code in ezesdk and elf.h.
A simple static analysis tool should be relatively straightforward at this point although to be useful it needs to do some more complicated things like determine dual-issue and so on. For that my guess is that i'll need a relatively complete pipeline simulator - it doesn't need to simulate the cpu instructions, just the register dependencies. A more dynamic analysis tool would require a simulator but I guess that's possible since the cpu is so simple (performance might be a factor at that point though).
But I don't really know and i'm just piss farting about - I haven't written tools like this for ... forever. Last time was probably a dissasembler I wrote in assembly language for the Commodore 64 about 25 years ago so I could dump the roms. Ahh those were the days. Actually these days aren't much different for me apart from different shit to be anxious about.
Productive enough afternoon anyway, I suppose i'd better go find some food and decide if i'm going to stay up to watch the soccer after watching some local footy and maybe the tour. 5am is a bit too late, or early, and tbh i don't really care too much who wins.
Update: Hacked a bit more last night, came up with a really shitty pipeline simulator.
From this code:
fmadd.l r0,r0,r0
fmadd.l r0,r0,r0
add r17,r16,r16
add r17,r16,r16
add r17,r16,r16
add r17,r16,r16
add r17,r16,r16
add r17,r16,r16
fmadd.l r0,r0,r0
rts
Assembled, then loaded from the elf:
de ra e1 de ra e1 e2 e3 e4
alu: - - - fpu: 0 fmadd - - - - -
alu: 1 add - - fpu: 1 fmadd 0 fmadd - - - -
alu: 2 add 1 add - fpu: 1 fmadd - 0 fmadd - - -
alu: 3 add 2 add 1 add fpu: 1 fmadd - - 0 fmadd - -
alu: 4 add 3 add 2 add fpu: 1 fmadd - - - 0 fmadd -
alu: 5 add 4 add 3 add fpu: 1 fmadd - - - - 0 fmadd
alu: 6 add 5 add 4 add fpu: 6 fmadd 1 fmadd - - - -
alu: 7 jr 6 add 5 add fpu: 6 fmadd - 1 fmadd - - -
alu: - 7 jr 6 add fpu: 6 fmadd - - 1 fmadd - -
alu: - - 7 jr fpu: 6 fmadd - - - 1 fmadd -
alu: - - - fpu: 6 fmadd - - - - 1 fmadd
alu: - - - fpu: - 6 fmadd - - - -
alu: - - - fpu: - - 6 fmadd - - -
alu: - - - fpu: - - - 6 fmadd - -
alu: - - - fpu: - - - - 6 fmadd -
alu: - - - fpu: - - - - - 6 fmadd
alu: - - - fpu: - - - - - -
The number infront of the instruction is when it entered the pipeline.
Oops, so bit of a bug there, once it dual-issues the first add/fmadd pair it just keeps issuing the ialu ops, which shouldn't happen. I've go the register dependency test in the wrong spot. I can fiddle with the code to fix that up but I need to find out a bit more about how the pipeline works because there some other details the documentation doesn't really cover in enough detail.
Update: After a bit of work on the house I had another look at the pipeline and did some hardware tests. So it looks like as soon as an instruction sequence arrives which might dual-issue, it gets locked into a 'dual issue' pair which will stall both instructions until both are ready to proceed - regardless of the order of the instructions and whether the first could advance on it's own anyway.
So for example, these sequences all execute as dual-issue pairs (all else being equal, there are other alignment related things but I haven't worked them out yet).
fmadd.l r0,r0,r0 fmadd.l r0,r0,r0 mov r16,r16 fmadd.l r0,r0,r0
mov r16,r16 mov r16,r16 fmadd.l r0,r0,r0 mov r16,r16
fmadd.l r0,r0,r0 mov r16,r16 mov r16,r16 mov r16,r16
mov r16,r16 fmadd.l r0,r0,r0 fmadd.l r0,r0,r0 fmadd.l r0,r0,r0
Anyway, so re-running the timing tool with these new changes give a better result:
alu: - - - fpu: 0 fmadd - - - - -
alu: 1 add - - fpu: 1 fmadd 0 fmadd - - - -
alu: 1 add - - fpu: 1 fmadd - 0 fmadd - - -
alu: 1 add - - fpu: 1 fmadd - - 0 fmadd - -
alu: 1 add - - fpu: 1 fmadd - - - 0 fmadd -
alu: 1 add - - fpu: 1 fmadd - - - - 0 fmadd
alu: 6 add 1 add - fpu: - 1 fmadd - - - -
alu: 7 add 6 add 1 add fpu: - - 1 fmadd - - -
alu: 8 add 7 add 6 add fpu: - - - 1 fmadd - -
alu: 9 add 8 add 7 add fpu: - - - - 1 fmadd -
alu: 10 add 9 add 8 add fpu: 10 fmadd - - - - 1 fmadd
alu: 11 jr 10 add 9 add fpu: - 10 fmadd - - - -
alu: - 11 jr 10 add fpu: - - 10 fmadd - - -
alu: - - 11 jr fpu: - - - 10 fmadd - -
alu: - - - fpu: - - - - 10 fmadd -
alu: - - - fpu: - - - - - 10 fmadd
alu: - - - fpu: - - - - - -
I also have another output format which is like the spu timing tool which shows each instruction in sequence with time horizontal. I don't have the correct labels yet but it shows the dual issue pairs more clearly. The register checking/writing might be in the wrong spot too but the delays look right.
fmadd dr1234
fmadd dr1234
add dr1
add dr1
add dr1
add dr1
add dr1
add dr1
fmadd dr1234
jr dr1
Still a few other details which can wait for another day.
Optimising
I spent a good chunk of yesterday trying to optimise the cexpi implementation to get of as many register access penalties as possible and dual-issue as many instructions as possible. There still seems to be a bit of magic there but i'm getting there.
what clock ialu fpu dual e1 st ra st loc fe ex ld
e_build_wtable 29637 21347 9548 8866 24 7563 21 36
e_build_wtable2 20149 17656 8184 6138 24 402 28 36
build_wtable_2 is based on the 5+4 term sincos from the previous post so requires fewer flops to start with but the main point of interest is the greatly reduced register stalls.
Primarily I just wasn't putting enough code between the flop instructions, but that can be easier said than done.
I used a technique I've talked about previously to be able to add more ialu instructions within the flops. Basically the loop is unrolled "in-place", whereby some results required for the next loop are calculated in the current one and otherwise the loop conditions remain the same.
A fairly detailed summation of the steps follows. This calculates two tables of sin/cos pairs together. The polynomial approximation is only valid over (0..pi/4) and so to calculate sin(pi/4+i) it calcualtes cos(pi/4-i) and so on.
build_wtable(complex float *wtable, int logN, int logStride, int logStep, int w0)
load constants
calculate loop count
loop:
all integer ops:
// 1: calculate frequency of this coefficient
f1 = w0 << shift
f0 = f1 * 2
// 2: calculate octant
j0 = f0 >> shift2
j1 = f1 >> shift2
// 3: calculate fractional part of frequency and mirror if required
x0 = f0 & mask;
x0 = j0 & 1 ? (scale - x0) ? x0;
x1 = f1 & mask;
x1 = j1 & 1 ? (scale - x1) ? x1;
// 4: calculate sign of result
negcos0 = ((j0+2) >> 2) << 31;
negsin0 = ((j0) >> 2) << 31;
negcos1 = ((j1+2) >> 2) << 31;
negsin1 = ((j1) >> 2) << 31;
// 5: determine if cos/sine needs swapping
swap0 = (j0+1) & 2;
swap1 = (j1+1) & 2;
All float ops:
// 6: scale input
a0 = to_float(x0) * 1.0 / scale;
a1 = to_float(x1) * 1.0 / scale;
// 7: calculate sin/cos over pi/4
b0 = a0 * a0;
b1 = a1 * a1;
... calculate sin'(a0/a1) and cos'(a0/a1) using fmadd+fmul
// 8: swap if necessary
cos0 = swap0 ? sin'0 : cos'0;
sin0 = swap0 ? cos'0 : sin'0;
cos1 = swap1 ? sin'0 : cos'0;
sin1 = swap1 ? cos'0 : sin'0;
// 9: fix sign
All Integer ops:
// twiddles bit-31 of ieee float
as_int(cos0) ^= negcos0;
as_int(sin0) ^= negsin0;
as_int(cos1) ^= negcos1;
as_int(sin1) ^= negsin1;
// a: output
*wtable++ = cos0 + I * sin0;
*wtable++ = cos1 + I * sin1;
// b: next step
w0 += wstep;
endloop
I wont show the detail of the calculation itself but I tried using Estrin's Algorithm for the polynomial expansion to try to reduce the latency involved. Actually it ended up a bit interesting because it shifted where the constants needed to be loaded for the 3-register fmadd (since it modifies it's first result, the constants need loading there) - and meant there were fewer ways to dual-issue instructions, more below. I might end up trying the other way too - but this stuff just sucks so much time it's crazy.
So basically there are a bunch of integer ops followed by float ops followed by a few int ops to finish off. Now comes the tricky bit where 'optimisation' comes into play. Firstly, float operations all have a latency which means that if you just use them in the order shown you wont get good performance.
Even just listing it the way I have is a simple optimisation.
For example:
a0 = to_float(x0) * 1.0 / scale;
b0 = a0 * a0;
a1 = to_float(x1) * 1.1 / scale;
b1 = a1 * a1;
Would take approximately 2x longer than:
a0 = to_float(x0) * 1.0 / scale;
a1 = to_float(x1) * 1.1 / scale;
b0 = a0 * a0;
b1 = a1 * a1;
If one looks at the basic instructions annotated with the delay slots it's pretty obvious which is better (i might be a off with the delay slots)
inline interleaved
float r8,r0 float r8,r0
- float r10,r1
- -
- -
- -
fmul r8,r8,r32 fmul r8,r8,r32
- fmul r10,r10,r32
- -
- -
- -
fmul r9,r8,r8 fmul r9,r8,r8
float r10,r1 fmul r11,r10,r10
-
-
-
-
fmul r10,r10,r32
-
-
-
-
fmul r11,r10,r10
But one can only do this optimisation if you have enough registers to fully calculate each separately (this is an important point, and why the cpu has so many registers).
The other factor is that the epiphany cpu can dual-issue certain sets of instructions in certain circumstances. Fortunately the circumstances are fairly simple (for the most part, some details still elude me) and it's basically a float + ialu or load op. The precise behaviour seems to depend on instruction order/alignment but i'm not really sure on all the details yet.
So this means for example that any of the integer operations can be interleaved with the float operations and effectively become 'zero cost' - assuming there is some 'fixed cost' based on the number of float ops and their scheduling requirements. Cool but it complicates things and dual-issuing instructions means you don't fill any of those latency slots so need to find more instructions!
Examining the algorithm there are some hard dependencies which force a particular calculation order but a bunch of the integer calculations aren't needed till the end.
- Steps 1-3
- These are required before any float ops can be performed. These cannot be dual-issued obviously.
- Steps 4-5
- These can be performed anywhere and they are not needed until the end. These are prime candidates for dual issue.
- Steps 6-7
- These are hard orderings that add float latencies which cannot be avoided. They also require some register moves to setup the 3-register fmadd instructions which can make use of some of those slots and dual-issue.
- Steps 8-a
- These are pretty much hard-dependencies on the output. Fortunately there are no ra penalties for integer operations but it does mean there is an integer/fpu op mismatch; as odd as it sounds it may actually help to convert these operations into floating point ops.
- Step b
- Can be put almost anywhere.
Actually ... I lied. All of those steps can be interleaved with others ... by calculating the value you will need for the next loop (or next next) instead. This requires a ton of registers - I used every 'free' register up and had to save a few to the stack besides. I think the epiphany ABI could use some tuning for size/performance but I don't have enough data to back up any changes; and it isn't simple because any change has side effects.
The algorithm then becomes changed to:
setup first loop
loop:
calculate result interleaved with setup next loop
The tricky bit comes in tracking the state of all the registers across the algorithm and ensuring the right value is calculated and in the correct register when it is needed. The simplest way to do this is to basically use a new register for every calculation that might be needed later and then bits of code can basically be re-arranged 'at will' without becoming too much of a complicated mess for a head to manage. And hope you don't run out of registers.
Still it's a little hard on the head and eyes so I'm thinking of writing a tool which can help with some of the work. I started with a tool that parsed the assembly and dumped a table of register liveliness; but then i realised to go any further with that i'd basically need to write a whole assembler so I started work on an instruction decoder that can pass over the compiled binary which should be easier. Epiphany's instruction set is fairly tiny so at least that shouldn't be too much work. Well i'll see on that one, ... it's still a lot of work.
Estrin's Method and 3-register FMA
So whilst doing a pass over this post I noticed the anomaly with the greatly reduced ialu count of the new implementation. I did notice when I wrote the initial implementation it seemed rather small compared to the previous one - I put it down to the reduced term count but on reflection is is more than that.
So the basic polynomial expansion using Horner's Rule for sin+cos() in terms of 3-register fmadd instructions becomes:
; sin
; a (A + a^2 (B + a^2 (C + a^2 D)
; r0 = a
; r1 = a^2
mov r2,rC ; t0 = C
1 fmadd r2,r1,rD ; t0 += a^2 D
mov r3,rB ; t1 = B
2 fmadd r3,r2,r1 ; t1 += a^2 (C + a^2 D)
mov r2,rA ; t0 = A
3 fmadd r2,r3,r1 ; t0 += a^2 (B + a^2 (C + a^2 D))
4 fmul r2,r2,r0 ; t0 *= a
; cos
; A + a^2 (B + a^2 (C + a^2 (D + a^2 E)
; r0 = a
; r1 = a^2
mov r2,rD ; t0 = D
1 fmadd r2,r1,rE ; t0 += a^2 D
mov r3,rC ; t1 = C
2 fmadd r3,r2,r1 ; t1 += a^2 (D + a^2 E)
mov r2,rB ; t0 = B
3 fmadd r2,r3,r1 ; t0 += a^2 (C + a^2 (D + a^2 E))
mov r3,rB ; t1 = A
4 fmadd r3,r2,r1 ; t1 += a^2 (B + (C + a^2 (D + a^2 E)))
Note that the cos 'A' is not the same as the sin 'A'. The digit infront of the fpu ops is the 'stage' of the calculation in terms of register dependencies.
The same using Estrin's Aglorithm:
; sin
; a ((A + a^2 B) + a^4 (C + a^2 D))
; r0 = a
; r1 = a^2
1 fmul r2,r1,r1 ; a^4 = a^2 . a^2
mov r3,rA ; t0 = A
mov r4,rC ; t1 = C
1 fmadd r3,r1,rB ; t0 = A + a^2 B
1 fmadd r4,r1,rD ; t1 = C + a^2 D
2 fmadd r3,r2,r4 ; sin'= (A + a^2 B) + a^4 (C + a^2 D)
3 fmul r3,r3,r0 ; sin = a sin'
; cos
; A + a^2 ((B + a^2 C) + a^4 (D + a^2 E))
; r0 = a
; r1 = a^2
1 fmul r2,r1,r1 ; a^4 = a^2 . a^2
mov r3,rB ; t0 = B
mov r4,rD ; t1 = D
1 fmadd r3,r1,rB ; t0 = B + a^2 C
1 fmadd r4,r1,rD ; t1 = D + a^2 E
2 fmadd r3,r2,r4 ; sin'= (A + a^2 B) + a^4 (C + a^2 D)
mov r4,rA ; t1 = A
3 fmadd r4,r3,r1 ; sin = A + a^2 ((A + a^2 B) + a^4 (C + a^2 D))
So 15 instructions vs 15 instructions, but 7 constant loads vs 5. Well that's interesting. With dual issue with this snippet the cost is hidden but if a routine has more ialu ops than flops then the latter leave more opportunities for scheduling.
Even if the instruction set had a 4-register fma instruction the second might be better due to needing one less stage of calculation.
ABI?
I wish the abi was tad bit more asm-hacker friendly. A compiler doesn't care where the spare registers are but keep track of the sparse ranges is a pain. I think it would benefit from having all 8 'zero page' registers available as scratch anyway.
I wouldn't mind something closer to this:
r0-r3 argument / saved by caller
r4-r7 gp / saved by caller
r8-r23 saved by callee / hardware (lr only) / constants
r24-r63 gp / saved by caller
Rather than this:
r0-r3 argument / saved by caller
r8-r11 saved by callee
r12 scratch / saved by caller
r13-r15 saved by callee / hardware
r16-r27 gp /saved by caller
r28-r31 constants
r32-r43 saved by callee
r44-r63 gp / saved by caller
I don't really see the need for any of the arm-legacy register assignments such as r12 == ip. This would leave 48 registers free for leaf functions (rather than the current 37) to use without having to resort to saving registers and importantly leave 0-7 which can have a huge impact on code-size. And it would still leave enough registers for outer loops and so on. The abi is designed to work with a cut-down cpu which i think has 16 registers: but the proposed would work there as well.
But yeah, who knows, any change isn't cost-free and if your code is calling lots of small functions rather than calling big processing leaf functions then it might not work so well (but yeah, it wont anyway). I previously tried patching gcc to modify the abi but I didn't fully complete it.
A better, faster sincos/cexpi
After posting about the fft implementation i've been working on to the parallella forums one kind fellow-hacker directed me to a tool which can be used to improve the error of polynomial estimates to functions. Basically to get the same or better result in fewer terms.
This gave me something to poke at for a couple of evenings but to be honest my maths skills are up shit creek these days and I had trouble working out a good approximation to cosine() or properly forming the expressions to take account of floating point precision limits.
So armed with knowledge of this new technique I did further searching and came across a few interesting papers/presentaitons from the PS2 era about function optimisation and floating point errors and then came across exactly the tool I was after sollya. So I compiled that up and had a bit of a play.
Once I worked out how it worked I did some analysis on the functions I created using lolremez, the ones I had, and some others I found on the net.
First, the 6-term expression I started with. SG(x) here casts the value to a float (C type).
> Z6=x*(SG(3.1415926535897931159979634685441851615906e+00)
+ x^2 * (SG(-5.1677127800499702559022807690780609846115e+00)
+ x^2 * (SG(2.5501640398773455231662410369608551263809e+00)
+ x^2 * (SG(-5.9926452932079210533800051052821800112724e-01)
+ x^2 * (SG( 8.2145886611128232646095170821354258805513e-02)
+ x^2 * SG(-7.3704309457143504444309733969475928461179e-03))))));
Warning: Rounding occurred when converting the constant "3.1415926535...
Warning: Rounding occurred when converting the constant "5.1677127800...
Warning: Rounding occurred when converting the constant "2.5501640398...
Warning: Rounding occurred when converting the constant "5.9926452932...
Warning: Rounding occurred when converting the constant "8.2145886611...
Warning: Rounding occurred when converting the constant "7.3704309457...
> dirtyinfnorm(sin(x * pi)-Z6, [0;1/4]);
2.32274301387587407010080506217793120115302759634118e-8
Firstly - those float values can't even be represented in single precision float - this is despite attempting to do just that. Given the number of terms, the error rate just isn't very good either.
I used lolremez to calculate a sinf() function with 4 terms, and then analysed it in terms of using float calculations.
> RS = x * ( SG(9.999999861793420056608460221757732708227e-1)
+ x^2 * (SG(-1.666663675429951309567308244260188890284e-1)
+ x^2 * (SG(8.331584606487845846198712890758361670071e-3)
+ x^2 * SG(-1.946211699827310148058364912231798523048e-4))));
Warning: Rounding occurred when converting the constant "9.9999998617...
Warning: Rounding occurred when converting the constant "1.6666636754...
Warning: Rounding occurred when converting the constant "8.3315846064...
Warning: Rounding occurred when converting the constant "1.9462116998...
> dirtyinfnorm(sin(x)-RS, [0;pi/4]);
9.0021097355521826457692679614674224316870784965529e-9
This is roughly 8x the error rate reported by lolremez or sollya with extended precision, but obviously an improvement over the taylor series despite using only 4 terms.
So using sollya to calculate an expression with the same terms whilst forcing the values to be representable in float is very simple.
> LS4 = fpminimax(sin(x), [|1,3,7,5|], [|single...|],[0x1p-16000;pi/4]);
> LS4;
x * (1
+ x^2 * (-0.1666665375232696533203125
+ x^2 * (8.332121185958385467529296875e-3
+ x^2 * (-1.951101585291326045989990234375e-4))))
> dirtyinfnorm(sin(x)-LS4, [0;pi/4]);
2.48825949986510374795541070830762114197913817795157e-9
So ... yep that's better. (0x1p-16000 is just a very small number since the calculation fails for 0.0).
One of the most accurate other implementations I found for sin() was from an article "Faster Math Functions" by Robin Green of Sony (cira ps2 era). The first term of this function is exactly representable in float and the constants calculated using remez. I analysed this in sollya.
> RGS = x * (1 + x^2 * (SG(-0.166666567325592041015625) + x^2 * (SG(0.00833220803) + x^2 * SG(-0.000195168955))));
Warning: Rounding occurred when converting the constant "0.0083322080...
Warning: Rounding occurred when converting the constant "0.0001951689...
> dirtyinfnorm(sin(x)-RGS, [0;pi/4]);
3.40294295123115698469497312067470829353049357459609e-9
Note that the first term is represented in floating point exactly.
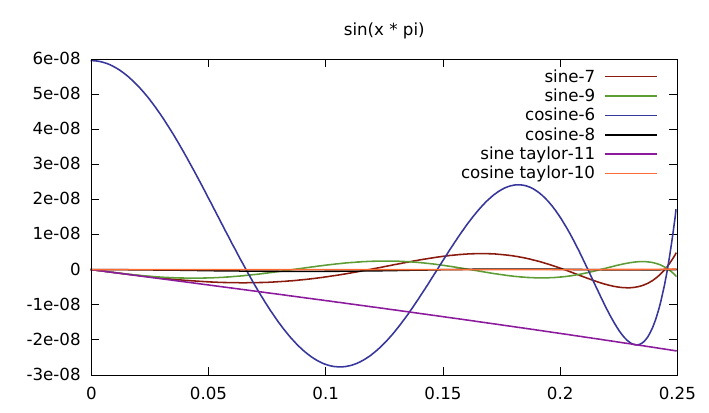
Plot time.
The lolremez version is faltering here because the first term is actually 1 in float, yet the optimisation process is assuming it has much higher accuracy and adjusting the other polynomial exponents appropriately.
> SG(9.999999861793420056608460221757732708227e-1);
1
I did some further mucking about with the tutorial which explained how to fix the first-term into one representable by floats (i.e. 1.0) but I wont include it here since it was superseded by the results from sollya with much less work (i.e. the result above). The one from the Robin Green article should be much the same anyway as it was derived in a similar manner.
cexpi()
So applying the problem to the one I was interested in - sin/cos with an integer argument, leads to the following solutions. By scaling the input value by pi, the full range is normalised to a 1.0, and powers-of-two fractions of one (as required by an fft) can be represented in float with perfect accuracy which removes some of the error during calculation.
> S4 = fpminimax(sin(x * pi), [|1,3,7,5|], [|24...|],[0x1p-16000;1/4]);
> S4;
x * (3.1415927410125732421875
+ x^2 * (-5.16771984100341796875
+ x^2 * (2.550144195556640625
+ x^2 * (-0.592480242252349853515625))))
> C5 = fpminimax(cos(x * pi), [|0,2,4,6,8|], [|24...|],[0;1/4]);
> C5;
1 + x^2 * (-4.93480205535888671875
+ x^2 * (4.0586986541748046875
+ x^2 * (-1.33483588695526123046875
+ x^2 * 0.22974522411823272705078125)))
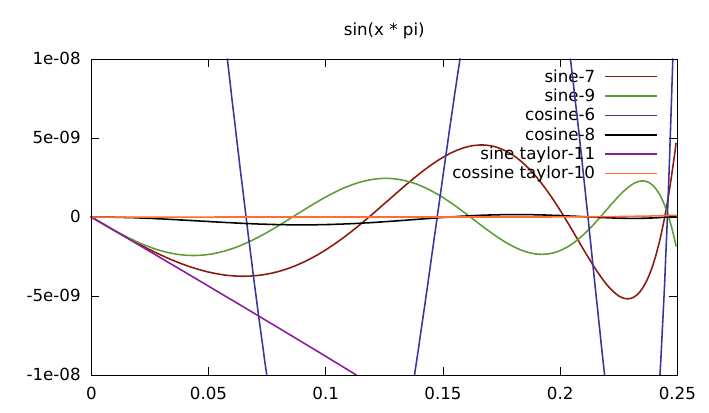
The reason for using 4 terms for sine and 5 for cosine is because at least 5 are needed for cosine for similar accuracy and it also creates a matching number of instructions since sine() needs the extra multiply by x - this also improves the instruction scheduling. Using more terms for sine only increases the accuracy by a small bit because this is hitting the limits of floating point accuracy so isn't worth it.
A closer view:
The taylor series for cosine is much better than the one for sine.
fmadd, fmul, etc
Most of the function can be implemented using multiply+add instructions if it is represented in the obvious 'Horner' form.
s = a A + a^3 B + a^5 C + a^7 D
= a (A + a^2 (B + a^2 (C + a^2 D)
c = 1 + a^2 A + a^4 B + a^6 C + a^8 D
= 1 + a^2 (A + a^2 (B + a^2 (C + a^2 D)
seq caclulation
0 a2 = a * a
1 s = 2.550144195556640625 + a2 * -0.592480242252349853515625
1 c = -1.33483588695526123046875 + a2 * 0.22974522411823272705078125
2 s = -5.16771984100341796875 + a2 * s
2 c = 4.0586986541748046875 + a2 * c
3 s = 3.1415927410125732421875 + a2 * s
3 c = -4.93480205535888671875 + a2 * c
4 s = a * s
4 c = 1.0 + a2 * c
Another way to represent the expression is using Estrin's method. I found this mentioned in the stuff by R.Green and he references Knuth.
This breaks the expression into independent sub-trees which can be calculated concurrently. This is obviously quite useful for SIMD calculations but can also be useful on a serial processor with a deep pipeline as it reduces the number of stages with serial dependencies.
s = a A + a^3 B + a^5 C + a^7 D
= a ( (A + a^2B) + a^4 (C + a^2 D) )
c = 1 + a^2 A + a^4 B + a^6 C + a^8 D
= 1 + a^2 ( (A + a^2 B) + a^4 (C + a^2 D) )
seq calculation
0 a2 = a * a
1 a4 = a2 * a2
1 s0 = A + a2 * B
1 s1 = C + a2 * D
1 c0 = A + a2 * B
1 c1 = C + a2 * D
2 s3 = s0 + a4 * s2
2 c3 = c0 + a4 * c2
3 s = a * s3
3 c = 1 + a2 * c3
This requires 1 more floating point instruction: but it executes in 3 stages of dependent results rather than 4. If latency of the calculation is important or if there are no other instructions that can be scheduled to fill the latency slots of the fpu instructions this would execute faster.
Exact floats: Hex Float Notation
Whilst looking through some code I came across the hexadecimal float notation which I hadn't seen before. I've been wondering how to correctly encode floating point values with exact values so this I guess is the way.
Sollya can output this directly which is nice, so the above expressions can also be represented (in C) as:
> display = hexadecimal;
Display mode is hexadecimal numbers.
> S4;
x * (0x3.243f6cp0
+ x^0x2.p0 * (-0x5.2aefbp0
+ x^0x2.p0 * (0x2.8cd64p0
+ x^0x2.p0 * (-0x9.7acc9p-4))))
> C5;
0x1.p0
+ x^0x2.p0 * (-0x4.ef4f3p0
+ x^0x2.p0 * (0x4.0f06ep0
+ x^0x2.p0 * (-0x1.55b7cep0
+ x^0x2.p0 * 0x3.ad0954p-4)))
So the hex number is the mantissa, and the exponent is relative to the decimal point in bits. It wont output expressions in IEE754 encoded values directly but they can be printed (useful for assembly).
> printsingle( 0x3.243f6cp0);
0x40490fdb
> printsingle(3.1415927410125732421875);
0x40490fdb
Goertzel's Algorithm
There are other ways to calculate series of sincos values quickly. One is Goertzel's Algorithm. It can calculate a series of sin/cos values of the form sincos(a + i*b), which is exactly what is required.
An example implementation:
float cb = 2 * cos(b);
// offset by 3 terms back
float ag = a - 3 * b;
// can be calculated using summation rule
float s1 = sin(ga+b);
float s0 = sin(ga+2*b);
float c1 = cos(ga+b);
float c0 = cos(ga+2*b);
// unroll the inner loop once to simplify register usage/reusage
for (int i=0;i<N;i+=2) {
s1 = cb * s0 - s1;
c1 = cb * c0 - c1;
s0 = cb * s1 - s0;
c0 = cb * c1 - c0;
out[i+0] = c1 + s1 * I;
out[i+1] = c0 + s0 * I;
}
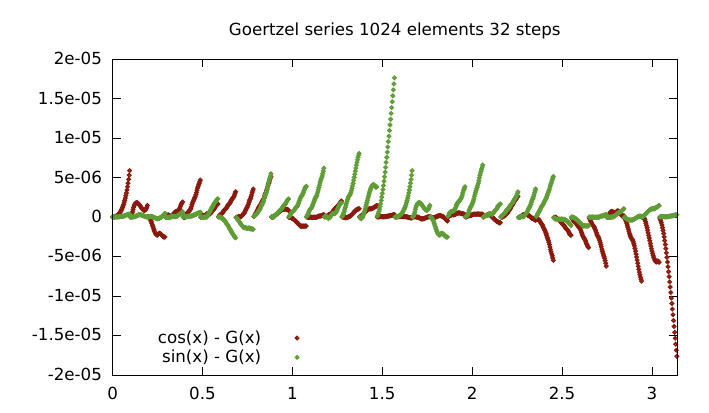
Unfortunately, floating point addition pretty much sucks so this will drift very quickly if cb*X is appreciably different in scale to Y in the cb*x-Y expressions. So error depend on both b and a, which leads to a funky looking error plot.
Where a = j*32*PI/1024 | j= (0 ... 31), b = PI/1024.
Was worth a try I guess.
Copyright (C) 2019 Michael Zucchi, All Rights Reserved.
Powered by gcc & me!