Object detector in action

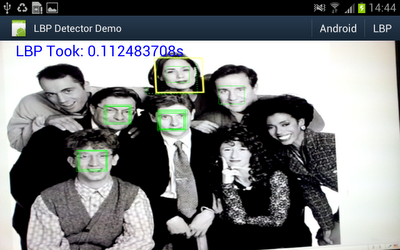
Well I really wanted to see if the object detector I came up with actually works in practice, and whether all that NEONifying was worth it. Up until now i've just been looking at heat-maps from running the detector on a single still image.

So I hacked up an android demo (I did start on the beagleboard but decided it was too much work even for a cold wintry day), and after fixing some bugs and summation mathematics errors - must fix the other post, managed to get some nice results.

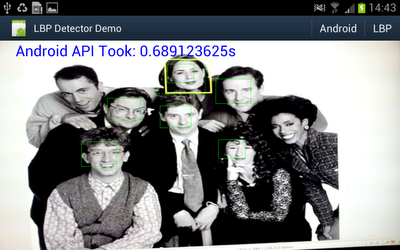
A bit under 10fps. And for comparison I hooked up some code to switch between my code or the android supplied one.

Well under 2fps.

I was just holding the "phone" up to a picture on my workstation monitor.

Some information on what's going on:

Device is a Samsung Galaxy Note GT-N7000 running ICS. This one has a dual core ARM cortex A9 CPU @ 1.4Ghz.
Input image is 640x480 from the live preview data from the Camera in NV12 format (planar y, packed uv).
Both detectors are executing on another thread. I'm timing all the code from 'here's the pixel array' to 'thanks for the results'.
The LBP detector is using very conservative search parameters: from 2x window (window is 17x17 pixels) to 8x window, in scale steps of 1.1x. This seems to detect a similar lower-sized limit as the android one - and the small size limit is a major factor in processing time.
At each scale, every location is tested.
Android requires a 565 RGB bitmap, which i create directly in Java from the Y data.
The LBP detector is just using the Y data directly, although needs to copy it to access it from C/ASM.
The LBP detector pipeline is mostly written in NEON ASM apart from the threshold code - but that should optimise ok from C.
A simple C implementation of the LBP detector is around 0.8s for the same search parameters (scaling and lbp code building still uses assembly).
The LBP detector is showing the raw thresholded hits, without grouping/post-processing/non-maximum suppression.
The LBP code is only using a single core (as the android one also appears to)
The LBP classifier is very specifically trained for front-on images, and the threshold chosen was somewhat arbitrary.
The LBP classifier is barely tuned at all - it is merely trained using just the training images from the CBCL data set (no synthesised variations), plus some additional non-natural images in the negative set.
Training the LBP classifier takes about a second on my workstation, depending on i/o.
Despite this, the false positive rate is very good (in anecdotal testing), and can be tuned using a free threshold parameter at run-time.
The trained classifier definition itself is just over 2KB.
As the LBP detector is brute-force and deterministic this is the fixed-case, worst-case performance for the algorithm.
With the aggressive NEON optimisations outlined over recent posts - the classifier itself only takes about 1 instruction per pixel.

A good 6x performance improvement is ok by me using these conservative search parameters. For example if I simply change the scale step to 1.2x, it ends up 10x faster (with still usable results). Or if I increase the minimum search size to 3x17 instead of 2x17, execution time halves. Doing both results in over 25ps. And there's still an unused core sitting idle ...

As listed above - this represents the worst-case performance. Unlike viola & jones whose execution time is dynamic based on the average depth of cascade executed.

But other more dynamic algorithms could be used to trim the execution time further - possibly significantly - such as a coarser search step, or a smaller subset/smaller scale classifier used as a 'cascaded' pruning stage. Or they could be used to improve the results - e.g. more accurate centring.

Update: Out of curiosity I tried an 8x8 detector - this executes much faster, not only because it's doing under 25% of the work at the same scale, but more to the point because it runs at smaller image sizes for the same detected object scale. I created a pretty dumb classifier using scaled versions of the CBCL face set. It isn't quite reliable enough for a detector on it's own, but it does run a lot faster.

The second golden age of personal computing.

With interest and some excitement (despite it being ~~Nokia~~ Nikon and having some negative experiences with them), I just read that Nokia have announce an Android powered camera. Of course, it's all ostensibly about feacebook and twatter, but one can easily see a world of more practical use to an appliance on which you can install customised software. Let's just hope that a DSLR isn't too far behind - although camera vendors may fear having the shift-ful proprietary software they took years to develop improved upon and obsoleted by someone else.

It is rather ironic that whilst desktop computer operating systems are locking down, dumb-stupifying and generally turning general purpose machines into appliances, appliance makers are opening up, complicating, and turning appliances into general purpose computers.

And at the heart of it, it's all thanks to Free Software. 'Onya RMS.

And it's no doubt also thanks to the purest form of capitalist economics. It is simply cheaper to use a free operating system than it is to write your own or purchase a per-appliance non-free one.

First Golden Age

I consider the first Golden Age of personal computers to the time before Microsoft Windows and their illegally attained `wintel' monopoly.

So these developments are clearly also a result of breaking the back of the wintel monopoly and the USA based global technology plutocracy.

Who would have thought that a bit of competition would benefit we the little people?

Second Golden Age

So I feel we're entering another 'golden age' of computing: where anybody with the skills can improve upon or replace the usually shitty software that comes with any device - as every device is now powered by substantial software components this equates to a lot of computers. With any luck I will never have to purchase a locked-down throw-away appliance ever again ...

However, I fear as with all golden ages, this one will also not last and eventually they will try to pull a M$ on us ...

First, vendors will start to lock down `internal' api's that give their own software an edge.
Then they will prevent non-authorised applications from being installed.
Eventually they will lock down the system so tight it returns to being a closed applicance.
All the while they will use lawyers as anti-competitive weapons.

Ultimately however economics will force their hand, and any such tactics will prove too costly to maintain.

But what cost to society will such experiments first extract?

Update: Thanks Sankar, yes Nikon, too much Tomi on my brain that morning. And of course, Samsung have followed up with announcing their Android camera ... yum.

Maths to the rescue

I had a bit of a think about the expression I am evaluating and I noticed I could use logarithms to perform the calculation instead of multiplies. And actually, as I don't use the value itself other than as a threshold, the summation result can be used directly anyway - it just wont give as sharp peaks.

First, changed the inner loop to perform a summation of two possible values, in 16 bits. This removed the need for 32-bit masks, and the floating point multiplies (not that they were holding anything up). This took 2 classifiers down from 26 instructions to 18, and a test-case from 100 to 70ms. It also freed 3 quad registers but I haven't yet investigated whether this will let me do more (actually it will let me take the loop down to 16 instructions as I have 2 immediate loads in there).

However, this morning I had a closer look at the summation I now have.

  r = sum m { testbit ? p : n }                        (1)

The bit testing code can't be further improved, but perhaps the select and sum can?

First, subtract n from the expression and move it outside of the select, and then separate the summation.

  r = sum m { (testbit ? (p - n) : 0) - n }
    = sum m { testbit ? (p - n) : 0 } - sum m { n }
    = sum m { testbit ? (p - n) : 0 } - mn             (2)

Which leaves with a slightly simpler internal summation and a constant. This expression can be implemented without a select instruction but since we have select in NEON it doesn't gain any instructions on it's own.

But this is where a neat trick of binary arithmetic comes in to play. Unlike C logic which uses 0 and 1 for false and true, the result of a bit test in SIMD code (and opencl c on vectors) is 0 for false, and ~0 for true. But in two's compliment signed binary, ~0 is also equal to -1.

So ... if the expression can be converted into a sum of -1's, then all one needs to do is directly add up the result of the bit tests, and avoid the select altogether. It is rather trivial to convert (2) into this form (if I have my summation identities on target anyway).

  r = sum m { (n-p) (testbit ? -1 : 0) } - mn
    = (n-p) sum m { testbit ? -1 : 0 } - mn
    = A sum m { testbit ? -1 : 0 } + B                 (3)

Where A and B are constants.

Actually there is another benefit here, as the summand is either 0 or -1 the range of the working sum is far more limited. Because of the size of the template I couldn't get away with 8 bit arithmetic without the danger of overflow - if I was using normal 8 bit two's complement arithmetic. But NEON to the rescue again, it has saturating instructions which will not overflow. It may still lead to a slightly incorrect answer - but i'm not interested in the absolute result but the relative one, and i think it should suffice.

I have yet to code this up, but if it works this will get the two-classifier case down to only 12 instructions - for 8 pixels. Less than one instruction per classifier per template, or about one when including the data loading as well.

And as this all now runs in double registers instead of quad registers, and I don't need n or p in the inner loop, it freeds up a whole swag of registers. These can be used to unroll more of the loop or share more of the data, for example by calculating more than 8 results per pass, more than one classifier at once, and so on. This might squeeze out a tad more juice out of it, but i'm not expecting much more here.

Update: So I coded it, it works. I'm calculating 32 locations at once, and there's still a good few registers free. Test case down from 70ms to 50ms.

Even better, I noticed the 'limited dual issue' capability of the NEON processor could be exploited in a couple of cases. Interleave the vtbl with some shifts: down to 43ms. Interleave the vqadd's with some vext's: down to under 41ms. Noice.

For comparison, an integer version in C (gcc, -O2) takes about 700ms.

Time for beer.

parallel 64 bit tests using NEON

So the next bit of code i've been working on requires a lot of 64-bit bit tests. Essentially using the tests as a 64-element 1-bit lookup table.

My first approach was to take an obvious C implementation, and convert it to NEON and perform the bit tests in parallel.

The C is basically like this:

  int i, count=0;
  for (i=0;i<N;i++) {
    uint64_t test = tests[i];
    uint64_t bit = (uint64_t)1 << bits[i];

    count += (test & bit) ? 1 : -1;
  }

It works, and one can perform the tests - but the tests need to be performed using 64-bit arithmetic - which takes a lot of register space, and a large amount of fuffing to get the data in the right format ('fuffing' is my technical term for data conversion/re-arrangement), and then the results must be converted back to 32-bits to form the selection masks.

So it's a great deal of code, much of which isn't doing anything but fuffing.

But the idea I had last night was to perform the testing using 8 bit values, and then scale these up to 32-bits to form the masks.

If one were writing the above code to avoid the 64-bit accesses in C, you could just use addressing to convert the 64-bit test to an 8 bit test - but on the correct byte instead.

  int i, count=0;
  for (i=0;i<N;i++) {
    int bitno = bits[i];
    uint8_t test = testsbyte[i * 8 + (bitno >> 3)];
    uint8_t bit = bitno & 7;

    count += (test & bit) ? 1 : -1;
  }

This requires per-byte addressing ... which you don't get for neon memory accesses per element ... except with vtbl.

So the following performs 8x 64-bit bit tests in only 5 instructions, and the actual tests are only using 8-bit arithmetic.

        @ d0 has 8 indices to test
        @ d1 has the 64-bit mask to test against
        @ d2 is set to 7 in 8 bytes
        @ d3 is set to 1 in 8 bytes
        
        vand.u8         d4,d2,d0        @ test & 7
        vshl.u8         d4,d3,d4        @ (1 << (test & 7))

        vshr.u8         d5,d0,#3        @ test >> 3
        vtbl.u8         d5,{d16},d5     @ data[test >> 3]
        
        vtst.u8         d4,d5           @ data[test >> 3] & (1 << (test & 7))

Changing the classifier to use code similar to this (but unrolled/scheduled better) gave me a 100% speed-up on the beagleboard (still unverified code ...).

Unfortunately, I still need nearly as many instructions just to convert the 8 bit mask into 32-bits for a selection mask (i need 32 bits for what i'm doing). But some mathematics might let me change that.

mipmap generation with SIMD/NEON

One part of the code i've been working on is building mipmaps so i can quickly generate non-aliased images at multiple scales.

This is an almost perfect fit for a SIMD processor, and in NEON it is no exception.

The simplest mechanism is successive averaging of a 2x2 blocks, and a simple C implementation which works ok is something like this:

void resample_1_2(uchar *src, uchar *dst, int sw, int sh) {
  int x,y;
  int dw = sw >> 1;

  for (y=0;y<sh;y+=2) {
    for (x=0;x<sw;x+=2) {
      uint v;

      v = (src[x+y*sw]
           + src[x+1+y*sw]
           + src[x+(y+1)*sw]
           + src[x+1+(y+1)*sw]) >> 2;

      dst[x/2+y/2*dw] = (uchar)v;
    }
  }
}

This can then just be called successively on the result from the previous run, until one reaches the desired depth.

This is easy to convert to SIMD, but some of the operations cannot be expressed in C or parallel variants, so it's easier just to show it in NEON. The only 'issue' to deal with is that NEON uses 8-byte memory accesses, but that isn't too difficult to cope with - we just produce at least 8 pixels at a time, i.e. 16 bytes input.

So the basic 1/2 downsample (actually it's 1/4) step is:

        @ Load 16x2 pixels
        vld1.u8         { d0, d1 },[r0],r1
        vld1.u8         { d2, d3 },[r0],r1

        @ Add horizontal adjacent pixels
        vpaddl.u8       q0,q0
        vpaddl.u8       q1,q1

        @ Add vertical adjacent pixels
        vadd.u16        q0,q1
        @ Average (/4)
        vshrn.i16       d0,q0,#2
        @ Output 8x1
        vst1.u8         { d0 }, [r2,:64],r3

The 'trick' here is the vpaddl instruction, which adds adjacent items in the vector and produces a result twice as wide, preserving all bits of precision. And the other trick is the vshrn instruction - shift right with narrow - which performs a shift and a cast to a half-sized result in one go.

The only problem with this is there just isn't enough work to do so the processor will be stalled some of the time. It also vastly underutilises the available resources. One obvious solution is just to go wider - take 32x2 pixels, and produce 16x1 results. A better solution is to go wider and deeper.

Since the data for the level above is already present in registers, one can save the memory load next time and just do the processing now. This can be extended as far as one has registers or as far as one wants to write specific custom code, but for me I just added another level.

So this is the final routine which takes a 32x32 pixel region, and generates two outputs: 16x16 1/2 downsampled, and 8x8 1/4 downsampled. Each loop generates 16x2 1/2 scaled results and 18x1 1/4 scaled ones - at full precision. (Actually again - these are 1/4 and 1/16 downsampled respectively since it does X and Y at 1/2 and 1/4 each, but you get the idea).

        @
        @ Rescale 32x32 bytes by 1/2 and 1/4
        @

        @ r0 = src
        @ r1 = width (stride)
        @ r2 = dst 1/2
        @ r3 = width/2 (stride)
        @ stack0 r4 = dst 1/4
        @ stack1 r5 = width/4 (stride)

        .global resample_12_14_neon

resample_12_14_neon:
        stmdb sp!, {r4-r6, lr}

        ldr     r4,[sp,#4*4]
        ldr     r5,[sp,#4*4+4]
        
        mov     r6,#8   @ for 32 input rows
        
1:      @ first 2 samples
        vld1.u8         { d0, d1, d2, d3 },[r0],r1
        vld1.u8         { d4, d5, d6, d7 },[r0],r1

        @ sum across
        vpaddl.u8       q0,q0
        vpaddl.u8       q1,q1
        vpaddl.u8       q2,q2
        vpaddl.u8       q3,q3

        @ sum down into 1/4 accumulation registers
        vadd.u16        q14,q0,q2
        vadd.u16        q15,q1,q3

        @ output 1/2 scale
        vshrn.i16       d0,q14,#2
        vshrn.i16       d1,q15,#2
        vst1.u8         { d0, d1 }, [r2,:64],r3

        @ Repeat for row 1
        vld1.u8         { d0, d1, d2, d3 },[r0],r1
        vld1.u8         { d4, d5, d6, d7 },[r0],r1
        
        vpaddl.u8       q0,q0
        vpaddl.u8       q1,q1
        vpaddl.u8       q2,q2
        vpaddl.u8       q3,q3
        
        vadd.u16        q0,q2
        vadd.u16        q1,q3

        @ Accumulate 1/4 scale
        vadd.u16        q14,q0
        vadd.u16        q15,q1

        vshrn.i16       d0,q0,#2
        vshrn.i16       d1,q1,#2
        vst1.u8         { d0, d1 }, [r2,:64],r3
        
        @ Generate 1/4 (1/16) scale
        vpaddl.u16      q14,q14
        vpaddl.u16      q15,q15

        vshrn.i32       d28,q14,#4
        vshrn.i32       d29,q15,#4

        vmovn.i16       d28,q14

        subs            r6,#1

        vst1.u8         { d28 }, [r4,:64],r5

        bhi             1b
        
        ldmfd sp!, {r4-r6, pc}

Of note perhaps is that the 1/4 result is generated in the high registers rather than use q4-q5. This is to honour the C ABI and avoid the need for saving these registers, only q4-q7 need to be saved.

It may be that the 32x32 access pattern is not ideal, and it requires appropriate padding/alignment of the mipmap levels, but I had more interesting things to look at so I didn't spend a lot of time on it.

One added benefit of doing the two levels at once is improved precision of the lower level since it doesn't use truncated intermediate results. For this reason it may be worth extending it to 3 levels, or 4 if registers allowed and the image stride restrictions weren't onerous. For VGA signals 3 levels of sub-sampling is adequate for what I need so it probably isn't worth going further than that.

Actually for this reason of precision, and the fact that I am usually down-sampling the scaled result from the mipmap, I decided the '2 row' version of the SIMD scaling routine would better suit my purposes. And the fact I had it already working helped ...

Classifier

So with all this I put together a timing routine for my classifier (I don't have the classifier itself setup yet/or debugged). The timing as usual depends a great deal on the scales one searches but, but when going from a scale of 0.207 to 0.333 in 6 steps (equating to an object width of 51 to 85 pixels for my 17x17 classifier), loading the mipmap, scaling to all the target scales and generating the LBPu2 codes takes about 5ms on the beagleboard-xm (image is 512x512). Which is pretty ok by me - even if I could squeeze a bit more out of it it's not going to be much.

The problem is now the classifier - when I turn that on it blows out to about 200ms (and most of that is at the smallest scale), or a pretty paltry 5fps (but of course, one must be-ware of timing on unverified code, it could be totally bogus). But I had a thought on that just before going to bed last night and I'm off to go see if i can't improve on that.

How to fuck up an operating system?

So I realised even the non-gnome image of Angstrom was still using systemd. The only reason seems to be that 'all the other distributions are using it'. Fuck off.

Well, I saw sysvinit was still there and installed that. But I noticed systemd was still being used as the preferred 'alternative' (sigh, another linux-invented fuckup of a system that is too). I fixed that to point to the proper init, but lo and behold, I had a broken system. Ahh, so that's why my narcisuss image didn't boot ... the offered option of init was merely an illusion.

The problem is that although the init scripts are there - they're mostly fucked up, and a huge chunk of shit is simply missing. Almost all of rcS is just not there.

So I see what's happened here - the systemd guys pretended to work on 'migrating' init scripts to systemd because they couldn't go the whole hog. You see, lower risk and all that. But what they were really doing is systematically vandalising the existing scripts - ones that worked and didn't need to be changed in years - so that they could never be used again for going back to the normal init. And when someone asks about init, they can claim the high moral ground by stating they did the work, and now "well it's up to you if you want to maintain the scripts" - and who is going to bother with that hassle? Of course, if they hadn't gone through and intentionally fucked them all up they wouldn't need any bloody maintenance to start with.

One should probably not attribute something to malice when incompetence would suffice, but it's hard to see this any other way.

Sigh.

Anyway, I managed to get some sort of fucked up version of a boot working. I added a couple of things to rcS:

mount -o remount,rw /
mkdir /dev/pts
mount -n /dev/pts

I also commented out the source of 'functions' from /etc/init.d/crond (they are provided by busybox).

That mostly works, although the network isn't activated properly - it starts but DNS isn't setup properly (i can ssh in, but emacs does some lookup at startup). A stop/start of the network fixes that, and with uptimes of weeks I think I can cope with that. It wont shutdown either, but what use is a filesystem it if can't handle the power going off or a reset button (There's also log rolling and other cron shit which has also been broken, but at this point I just don't care).

gateone

What the fuck is this shit? According to the package description it's a HTML5 terminal emulator. Why is that even installed on an embedded computer, and why is it automatically started and chewing up resources for no good reason?

Totally bizarre.

emacs

I have a feeling my sluggish-as-fuck emacs had more to do with whatever the hell 'gateone' is than systemd or anything else - but I can't be certain, nor do I particularly care for the specifics (possibly both - they were always both at the top of the process table, low cpu usage, but always running). I got rid of both and my problems also not-so-magically disappeared (hah ... funny that).

So with all that done, the whole system and emacs in particular is actually usable from a remote ssh login (but not emacs over X, because the gtk guys in their infinite wisdom decided client-side text rendering is the way to go - which pretty much killed the usefulness of remote X in one swooping fowl a few years ago).

So no more random pauses of up to half a second just because the system decided I was getting too much done.

And it even boots faster! Even if it's only because almost nothing is started apart from networking, getty, and sshd - but funny, that's all I thought it was starting anyway.

And so, the answer to the question in the title is obvious: let someone who hates the entire design and philosophy of the operating system replace it's core components, one at a time.

SIMD linear re-sampling

It's usually more efficient to do bi-linear re-sampling in two passes as it then only requires 2 multiplies per output pixel rather than 4. So today I had a look at the X sampling problem in SIMD - as re-sampling in Y is a trivial SIMD exercise.

I've done this before in SPU, but I couldn't find my code again, and in any event it wasn't so much the algorithm as the NEON translation that was the tricky bit.

A simple and efficient way to implement this re-sampling in C is to use fixed point 16.16 bit values for the calculation (this is more than enough accuracy for screen-resolution images), so a straightforward implementation is something like the following:

float scale = (float)srcwidth / dstwidth;
uint xinc = (int)(65536 * scale);
uint xoff = 0;
int x;

for (x=0;x<dstwidth;x++) {
   // pixel address
   uint sx = xoff >> 16;
   ubyte a = src[sx];
   ubyte b = src[sx+1];
   // pixel fraction
   uint rx = xoff & 0xffff;

   dst[x] = (ubyte)(a + ((b-a) * rx) >> 16);

   xoff += xinc;
}

This assumes the scale factor is >= 0.5, and bi-linear re-sampling breaks down outside of such scales anyway.

For RGBA data, converting this to SIMD is straightforward, all the calculations are simply extended to 4 wide vectors (if that is the machine size). But for greyscale this doesn't work because each position needs to be loaded independently.

The approach I came up with is to use a table lookup instruction to extract N consecutive pixel values into A and B vectors and then use per-lane scale factors. I also saw this guy did it very differently - using a transpose so that the problem is always the easily-SIMD y case.

Pseudo-code is something like this (using some opencl constructs):

float scale = (float)srcwidth / dstwidth;
uint xinc = (int)(65536 * scale);
uint4 xoff =  { xinc * 0, xinc * 1, xinc * 2, xinc * 3 };
int x;

for (x=0;x<dstwidth;x+=4) {
   // pixel address
   uint4 sx = xoff >> 16;
   ubyte8 d = vload8(src, sx.s0);
   // pixel fraction
   uint4 rx = xoff & 0xffff;
   // form lookup table
   uint4 ox = sx - sx.s0;

   ubyte4 a = lookup(d, ox);
   ubyte4 b = lookup(d, ox+1);

   vstore4(dst, x, (ubyte4)(a + ((b-a) * rx) >> 16));

   xoff += xinc * 4;
}

Where lookup takes the first argument as an array of elements, and the second a list of indices, and it returns a lookup of each index from the array. The limited lookup-table suffices, since the limited scale range prevents out-of-range accesses.

The astute reader will notice that this requires unaligned memory accesses for loading d, but with some small changes it could cope with forced-aligned memory accesses which is probably worth it. Actually the only change required is to use a aligned (masked) sx.s0 for the load and ox calculation.

In the NEON code I mixed it up a bit - the sx.s0 calculation I performed in ARM code (as it's needed for indexing lookups) as well as sx being calculated in NEON. But the scaling itself (and rx) uses 8.8 fixed-point so that 16-bit multiplies suffice. And 8 bits is enough precision for the pixel interpolation.

I tested scaling half a 512x512 image (i.e. 256x512) up by 2x in X to 512x512. Machine is a Beagleboard XM with default CPU clocking. I'm just using a C routine to call the assembly which processes one row at a time.

Routine         Time (ms)
C                9
NEON             2.9
NEON 2x          1.7
NEON 4x          1.5

The NEON code is processing 8 pixels at a time (minimum transfer size of NEON load).

One problem with the straight conversion of the above code to NEON is that there are many dependent instructions/stalls/no dual issue opportunities. So the 2x and 4x versions process 2 and 4 rows of data concurrently and interleaved. Apart from the better scheduling it also allows the addressing and rx calculations to be shared.

I also tried the masked version and aligning the reads and writes, I thought that gave better results - but it was only an error (i'd changed the scale factor). Although adding an appropriate alignment specifier to writes did make a stable measurable (if small) difference.

Y Scaling

I haven't looked at Y scaling but that is fairly straightforward. Actually rather than perform a complete X scale pass and a complete Y scale pass it's betterto scale the (Y, Y+1) rows into a double-row buffer, and then form the output one row at a time. Actually this can be extended to a pipeline of processing if you need to implement further passes and don't need all the data for a given pass - I used this in ImageZ to perform floating point compositing of integer data very fast in Java. This requires much less temporary memory, and should be faster because of the cpu cache (and see below about how slow memory is and how much the cache is needed). Actually since you're normally scaling up by some amount, Y(n+1) will probably be equal to Y(n)+1, so you can save some the X scaling work as well.

For this reason the 2x version is probably more useful even if it isn't the fastest. In fact it can just perform the Y scaling directly in-register and avoid the temporary buffer entirely. The overheads of calculating the same row more than once might be offset by not needing to pass intermediate results through memory.

I noticed that everything seems to take about 1ms + a bit. I wonder what the memcpy time is ... ok, just using memcpy on each row (512x512) is over 1.2ms. Wow, that's slow memory. I will have to try this on the Mele (which I still haven't had time to play with much) and the Tegra 3 tablet when I get it back. I gotta say the machine is running like a pig - emacs (terminal mode) crawls on it over the network with constant pauses and delays - it feels worse than running it via a 56k modem on an Amiga 1200. Maybe something is up with the network (looks like it, console seems a lot better) ... probably the old ADSL router which is causing other issues besides (can't turn off the dhcp server, which is affecting a couple of machines).

mip-maps

So I mentioned earlier that the above scaling routines only handle scaling by >= 0.5. So how does one go smaller? Either "do it properly" by implementing an "upfirdn" function (up-sample, filter, down-sample) - which is really just a 'sparse' convolution, or you approximate it with a mip-map.

i.e. you just pick the best-closest mipmap, and then scale that down/up to fit the output. Although building a mipmap is pretty fast it is still an overhead, so it helps if you are going to use it more than once - which is the case with sliding window object detectors which must run at multiple scales.

Although there are better ways to build the mipmaps (i.e. using the upfirdn stuff), using successive summation/a box filter works well enough for what I need. It can also be implemented rather neatly in NEON - I can perform a 1/2 and 1/4 scale scaling in the same routine (and there are enough registers to do 1/8th - but that requires 64-pixel-horizontal blocks).

I didn't bother trying to implement it in C, but the NEON code I wrote can re-sample a 512x512 image into two scales - 256x256 and 128x128 in under 1.3ms by processing 32x32 tiles. One then calls this successive times on the smallest result to build the rest, at least down to 8x8 (which is more than I need).

I've ignored the edge cases for now ... and usually it's better just to arrange ones data so that there aren't any. i.e. by aligning the stride and allocating extra invalid rows. The only problem with this is with getting data from/to external sources/destinations that may have their own alignment restrictions/policies. Obviously one wants to avoid a dumb memcpy but usually there's some work that can be done, and then the edge cases only need to be handled at these interfaces.

Update: I didn't have much to do today whilst waiting for a meeting, so I mucked about with the hardware today - tried to use a narcissus image - but that wouldn't boot, so just changed to a faster SD card I bought on the way back from buying milk & beer sugars (gee, sd cards are cheep now), ethernet cable, and different switch - and after that it's still slow in emacs ... But I also mucked about with the mele and got my test harness running there. Most of the stuff is 1.5x to 2x faster than the Beagleboard XM - which is pretty nice. The mipmap code is about 4x faster!

Update 2: Late last night I poked again - I thought I had enough to put it all together but then I realised I hadn't written the XY scaling. I tried adding Y interpolation to the Xx2 row scaler, but that just took twice as long to run as it ends up doing twice as many rows (stating the bleeding obvious). It still might be useful as it requires no temporary memory but I will work on another approach using temporary row buffers which I know works well.

Update 3: Well there's no particular reason I didn't include the NEON code ... so here it is. This is just the 1x version which isn't particularly quick due to data stalls and conflicts - but it can be extended obviously by unrolling the loop and interleaving the operations.

        @
        @ Scale row in X.
        @

        @ r0 = src address
        @ r1 = dst address
        @ r2 = width of output
        @ r3 = scale factor, 16.16 fixed point

        .global scalex_neon
scalex_neon:
        stmdb sp!, {r4-r7, lr}
        
        @ copy over scale
        vdup.32         q2,r3

        @ xinc = { scale * 0, scale * 1, scale * 2, ... scale * 7 }
        vldr    d0,index
        vmovl.u8        q3,d0
        vmovl.u16       q0,d6
        vmovl.u16       q1,d7

        @ xoff [0 .. 3]
        vmul.u32        q0,q2,q0
        @ xoff [4 .. 7]
        vmul.u32        q1,q2,q1
        @ xinc = 8 * inc
        vshl.u32        q2,#3

        vmov.u8         d28,#1
        
        @ xoff(s) = 0
        mov     r4,#0

        @ Load this, next
1:      add     r5,r0,r4,lsr #16
        vld1.u8 { d16,d17 }, [r5]

        # sx = xoff >> 16
        vshrn.u32       d18,q0,#16
        vshrn.u32       d19,q1,#16
        vdup.u16        d20,d18[0]

        @ mx = sx - sx[0]
        vsub.u16        d18,d20
        vsub.u16        d19,d20

        @ convert to 8 bits - this is lookup table for all 8 entries
        vmovn.u16       d18,q9

        @ a = src[sx]
        vtbl.8          d20,{d16,d17},d18
        @ b = src[sx+1]
        vadd.u8         d18,d28
        vtbl.8          d22,{d16,d17},d18

        @ rx = (xoff & 0xffff) >> 8
        @ (only need 8 bits for lerp)
        vmovn.u32       d24,q0
        vmovn.u32       d25,q1
        vshr.u16        q12,#8
        
        @ convert to short for arithmetic
        vmovl.u8        q10,d20
        vmovl.u8        q11,d22

        @ (b - a) * rx
        vsub.u16        q13,q11,q10
        vmul.u16        q13,q12

        @ (((b-x)*rx) >> 8) + a
        vshr.s16        q13,#8
        vadd.u16        q13,q10
        
        @ convert back to bytes
        vmovn.u16       d26,q13

        @ done
        vst1.u8 d26,[r1]!

        @ xoff += xinc*8
        add     r4,r3,lsl #3
        @ xoff += xinc
        vadd.u32        q0,q2
        vadd.u32        q1,q2

        @ for whole row
        subs    r2,#8
        bhi     1b
        
        ldmfd sp!, {r4-r7, pc}

        @ per-byte pixel offsets/multiplicands
index:  .byte   0,1,2,3,4,5,6,7

About Me

Tags

Internode Streaming Radio App