About Me
Michael Zucchi
B.E. (Comp. Sys. Eng.)
also known as Zed
to his mates & enemies!
< notzed at gmail >
< fosstodon.org/@notzed >

e-port revisited
I can't remember if i posted this here or just discussed it on the forums, but here's an update on the 'eport' code. eport is a lightweight 1:1 synchronisation point designed to assign owneship of slots in a cyclic buffer with minimum overhead. This directly allows the utilisation of some of the specific features in the epiphany architecture.
Since I can't find the post (probably just a bad subject) here's an overview of the api:
- int eport_reserve(eport *)
- Reserves a single slot in the port for the writer. The returned index is the slot number. Once this returns the writer has exclusive access to the given slot.
- void eport_post(eport *)
- Indicates that a slot previously reserved is now owned by the receiver with the implication that it contains valid data. Slots are automatically cycled in the same order they are reserved.
- int eport_wait(eport *)
- Waits for data to be ready at the receiving end. The return value indicates the slot number.
- void eport_done(eport *)
- Marks the next slot free to be re-used by the caller.
Ok so my initial implementation used power of two sizes for the indices for efficiency reasons of the cyclic buffer index calculation (modulo) and it only required 2 'pointer' values. However, because of repeating of the cycles one of the slots always sits unused, and furthermore the forcing of a power-of-two size can easily lead to needing to allocate more space than is necessary to implement an algorithm. There just isn't enough space to waste like this. An additional problem I hit when working on a real application was that the implementation required that every reserve be paired directly with a post, and every wait be paired directly with a done - which precluded the ability to use multiple slots in the buffer at once - which was kind of the whole point of it!
So I had a fiddle and came up with a new implementation which manages to allow all slots to be in use and also allows for arbitrary sizes without an expensive modulo operation. It only needs two extra local 'pointers' which are used to track multiple outstanding reserves/waits properly. If memory is tight the receiver can limit the working-set to exactly the amount it requires, or allow one extra free slot to allow for interleaving of work.
I've only just banged it up so it might not be correct or handle all the edge cases, but here it is anyway.
data structure
// Code Copyright (C) 2013 Michael Zucchi
// Licensed via GNU GPL version 3 or later.
struct eport {
volatile unsigned int head;
volatile unsigned int tail;
unsigned int index;
unsigned int next;
unsigned int size;
struct eport *other;
};
Each of these is allocated in pairs - one local to the sender and one local to the receiver. other pointers to the other one of the pair and everything else apart from size is initialised to 0. The only cross-communication is that the sender updates head in the receiver, and the receiver updates tail in the sender - obviously an atomic operation with no round-trip required.
index is local to each end and tracks the next slot, modulo the size of the cyclic buffer. Likewise next indicates the next 'actual' slot being requested at each end.
reserve
unsigned int eport_reserve(struct eport *port) {
unsigned int next = port->next;
// Check for a free slot
while (next >= port->tail + port->size) {
EPORT_SLEEP();
}
port->next = next + 1;
// Increment index modulo size
unsigned int r = port->index;
port->index = (r+1) == port->size ? 0 : r+1;
return r;
}
Because the "pointers" run without modulo I can simplify the capacity test. I then manually keep track of the index modulo the size for use by the caller. By using next to track the allocation it detaches the allocation from the publishing so it properly handles multiple outstanding reserves.
EPORT_SLEEP() does nothing on epiphany but might call usleep(x) on GNU/Linux.
post
void eport_post(struct eport *port) {
unsigned int h = (port->head + 1);
port->other->head = h;
port->head = h;
}
Post is basically the same as it was before, except now it doesn't need to modulo the pointer. Since the slot is known to be owned by the sender all it has to do is update the pointers at both ends. The sender is the only thread that can write to head so it needs no arbitration.
reserve
unsigned int eport_wait(struct eport *port) {
unsigned int next = port->next;
while (port->head == next)
EPORT_SLEEP();
port->next = next + 1;
// Track tail % size
unsigned int r = port->index;
port->index = (r+1) == port->size ? 0 : (r+1);
return r;
}
There is some obvious (and nice) symmetry with the reserve function here in the receiver. Again next is used to detatch acceptance from recycling.
done
void eport_done(struct eport *port) {
unsigned int t = (port->tail + 1);
port->other->tail = t;
port->tail = t;
}
Done is similarly symmetric to the post function. And here the receiver is the only one who can ever write to tail, so it needs to also needs no arbitration.
summary
So in short ... eport
- Allows for lock-free, ordered synchronisation of a fixed number of buffers between two cooperating cores;
- Allows for fully sychronous or n-buffered operation;
- Lightweight - only a single memory write is required at each post or done call.
When coupled with epiphany's blocking-free writes and limited memory it allows one to write streaming processors which write directly to the target core without needing any additional synchronisation and potentially asynchronously.
One drawback of the implementation above is that a given port is limited to 2^32-1 operations at a time before the maths breaks down, although that could be addressed by using 64-bit integers or some more complex pointer arithmetic.
I'm pretty much done for today but this is just another small step toward getting the 1-pass image scaler going. I think it should also end up a reasonable basis for writing a 1-pass 2-d separable convolution, wavelets, and so on. For some reason although i'm just a little bit of work away from finishing it I keep putting it off - today it's that the wind kept me awake all night and i'm too knackered to think straight. e.g. althogh i haven't compiled or debugged it I have the whole 2-d bicubic scaler written, I just need to slot in this updated eport code. Another day.
On another note i'm finally on xmas leave - hopefully for a few months like last year but I have a feeling i'm going to get roped in to doing a bit of other work which might cut it short. At this point i have a head full of ideas to code on but i think for sanity's sake I will need to take a break at some point too.
Wondered why the cartoons were on telly so late ...
Oops, it's early not late. Somehow it got to 5am, and now it's nearly 6.
I was looking up Welsh accent videos after watching 'Utopia' on SBS along with a bottle of red and a couple of rum on ices and somehow 6 hours vanished before I had realised. Probably didn't help that I only had cheese, olives, and other pickled condiments for dinner. It all seemed like a good idea at the time.
The last few weeks i've been working extra hours to try to burn out my contract before the xmas break so I was already a bit wiped out and I think I got a bit over-eager from wanting it to be over. Insomnia, poor sleep in general and even some annoying 'dreams' about bit reversal permute and vertical fft algorithms just compounded this. Got a meeting in a few hours - but it's only really a hand-off of pre-prepared work and i'm sure I can burn an iso or two.
I guess i'm just really looking forward to a couple months off and started a bit early. Just 16 hours left and all my main tasks are done for the contract and i'm pretty much over it at this point. But a big component is a few of those 'never ending' research-oriented tasks that have no defined completion milestones so I still have plenty to poke at.
Hmm, forcecast is 43 today - garden will be incinerated. It was forecast 41 yesterday and from the look of the plants I can't tell if i'm waterlogging them or letting them dry out too much - I dumped a few hours worth of rainwater tank on the garden trying to help it survive. Need some spot shades to stop the exteremeties burning off since it's a lot hotter than that in the full sun on the bare earth or on the black polyethelyne picking buckets I'm using as pots for the herbs. Last year I measured over 70 on a wheelie bin and that wasn't even in full sun all day. Even the birds are barely singing well after sun-up - must know what's coming in a few hours.
Better try to get a couple of zed's - can always sleep the arvo off. Damn eyes are killing me too as they have been for few weeks; bloody hayfever and i can't be far away from needing glasses.
Android icon lists
I was hitting some performance / usability issues with a list of icons (sigh, again) ... and looking at the code I came up last time I just don't know what I was thinking. In part it stemmed from initially using an adapter without customising the view; so i was forced to use a standard ImageView.
Anyway, I think ... i finally worked out a relatively clean solution to a listview which contains images which are loaded asynchronously.
In short:
- Create a sub-class of ImageView and use that wherever an icon in a list is used.
- Implement a separate loading/cache which loads images at the direction of this new ImageView via a thread. It needs to be able to throw away requests if they're not needed and generally serialise loading of images.
- Just set the image uri/url/file on the ImageView and let it handle aborting load of an image if it didn't use it.
- And this is the important bit which gets around an annoying problem with android: treat item 0 separately and just load it's icon directly w/o caching.
Without the last item you can end up loading the the image into the wrong imageview so end up with a missing icon - I recall having a lot of problems trying to workaround this last time, but this is a much more reliable and simple solution.
Previously I was trying to use notifyDataSetChanged() each time an image loaded as well as other nasty redirections to try and update properly whilst still coping with android (ab)using item 0 for it's own nefarious purposes (i presume it's for layout).
Originally i needed to load remote url's so I couldn't just use setBitmapURI() (otherwise i probably would've just used that at the time - it was a very short-on-time prototype), and although i currently don't need that functionality this manual code is smoother for the user and I can do other stuff like animations. The android code will delay drawing the screen until the image is actually loaded which adds a lot of judder particulalry if you're images might be large sizes.
Still not as nice as the JavaFX stuff I did, but it'll suffice. I will have to do something similar in the internode radio app - the solution there is different again but not very good either.
FFT bit-reverse, NEON
Hacked up a NEON version of the FFT permute I mentioned in the last post. Because it worked out much simpler to code up I went with the blocked-8 8-streaming version. Fortunately ARM has a bit-reverse instruction too.
Actually it ended up rather elegant; although i need to use 9 separate addresses within the inner loop, I only need to explicitly calculate one of them. The other 8 are calculated implicitly by a post-increment load thanks to being able to fit all 8 into separate registers. The destination address calculation still needs a bit reversal but 3 instructions are enough to calculate the target address and index to the next one.
This leads to a nice compact loop:
1: rbit r12,r11
add r11,r3
add r12,r1
vld1.64 { d16 },[r0]!
vld1.64 { d17 },[r4]!
vld1.64 { d18 },[r5]!
vld1.64 { d19 },[r6]!
vld1.64 { d20 },[r7]!
vld1.64 { d21 },[r8]!
vld1.64 { d22 },[r9]!
vld1.64 { d23 },[r10]!
subs r2,#1
vstmia r12, {d16-d23}
bne 1b
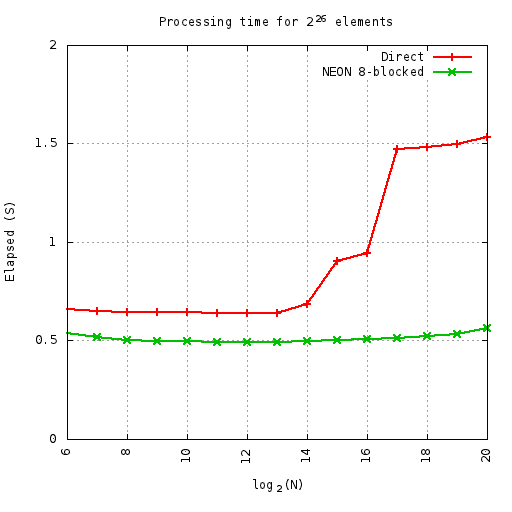
Despite this elegance and simplicity, compared to a straightforward C version the performance is only a bit better until the cache gets overflown.
At least on this machine (parallella-16 - the ARM side) the benefits of the cache-friendly code are measuable and start at 32K elements.
Here i'm runnning so many cycles of the given permute, where the number of cycles x N = 226 - i.e. always doing the same number of total elements. This equates to 1M iterations at 64-elements. All elements are complex float. This means the smaller sizes do more loops than the larger ones - so the small up-tick on the ends is first from extra outer loop overheads, and then from extra inner loop overheads.
Also hit a weird thing with the parallella compiler: by default gcc compiles in thumb mode rather than arm.
Update: So I found out why my profiling attempts were so broken on parallella - the cpu gouverner.
# echo performance > /sys/devices/system/cpu/cpu0/cpufreq/scaling_governor
Fixes that. It also makes emacs a lot smoother (I was wondering why text-mode emacs across a gig-e connection was lagging so much). I was running some timings on a C implementation of Cooley-Tukey and noticed some strange results - it turned out the scheduler was only kicking in once the problem got big enough so time-per-element turned into a saw-tooth.
Actually I re-ran the above plot and although the numbers did change a little bit they were only minor. Oh, I also added alignment specifiers to the vld1 instructions - which made a small but significant difference. I then tried doubling-up on the above function - forming 16 consecutive output cfloat results. But this was consistently slower - I guess hitting 2x the width on output is causing more cache thrashing (although i'm not sure why it's slower when running in-cache).
Some noise woke me up around 2am and I ended up getting up to have something to eat and then hacked until sunrise due to insomnia (pity Sunday is the mowing day around here - so now i'm grumpy and tired and need to do my own noise-making in the back yard soon). I did the timing stuff above and then looked into adding some extra processing to the permute function - i.e. the first couple of stages of the Cooley-Tukey algorithm. NEON has plenty of registers to manage 3 stages for 8 elements but it becomes a pain to shuffle the registers around to be able to take advantage of the wide instructions. So although i've nearly got a first cut done i'm losing interest (although simply being 'tired' makes it easy to become 'tired of' anything) - parallella will remove the need to fuck around with SIMD entirely, and there isn't much point working on a fast NEON FFT when ffts already exists (apart from the for-the-fun-of-it exploration). Well I do have a possible idea for a NEON implementation of a "vertical" FFT which I will eventually explore - the ability to perform the vertical portion of a 2D fft without a transpose could be a win. Because of the data-arrangement this should be easier to implement whilst still gaining the FLOP multiplier of SIMD but there are some other complications involved too.
FFT jiggery pokery
I've been meaning to poke at FFT calculation for a while and I finally got around to having a proper look.
First I just needed to calculate a single value so I did it by hand - I got some strange profiling results from Java vs jtransforms but it turned out that due to it's complexity it takes many many cycles before the JIT fully optimises it.
Then i started looking from a trivial Cooley-Tukey implementation that allocated all it's output arrays ... and i was surprised it was only about 1/2 the speed of jtransforms for it's simplicity. I tried a few variations and delved a bit into understanding the memory access patterns - although after an initial bit-reversed premute the memory patterns are trivial. It was still stuck at about 1/2 the speed of jtransforms.
I had a bit more of a think about the bit-reversing memory permute stage and figured it wouldn't work terribly well with cpu caches. First I just worked on blocking the output by 8 elements (=1 cache line) toward re-arranging the reads so they represent 8 sequential streams. Strangely enough this second case is a bit slower on small workloads that fit in the cache although is a bit faster on larger ones. It's not really much of a difference either way.
D:d |S:s | 0
D: d |S: s | 16
D: d |S: s | 8
D: d |S: s | 24
D: d |S: s | 4
D: d |S: s | 20
D: d |S: s | 12
D: d |S: s | 28
D: d |S: s | 2
D: d |S: s | 18
D: d |S: s | 10
D: d |S: s | 26
D: d |S: s | 6
D: d |S: s | 22
D: d |S: s | 14
D: d |S: s | 30
D: d |S: s | 1
D: d |S: s | 17
D: d |S: s | 9
D: d |S: s | 25
D: d |S: s | 5
D: d |S: s | 21
D: d |S: s | 13
D: d |S: s | 29
D: d |S: s | 3
D: d |S: s | 19
D: d |S: s | 11
D: d |S: s | 27
D: d |S: s | 7
D: d |S: s | 23
D: d |S: s | 15
D: d|S: s| 31
This shows the source-destination read/write pattern for a bit-reversal permute. Obviously with all those sparse reads the cache coherency isn't going to be great. FWIW moving from s to d (sequential writes) proved to have better performance than from d to s (sequential reads).
D:dddddddd |S:0 4 2 6 1 5 3 7 |
D: dddddddd |S: 0 4 2 6 1 5 3 7 |
D: dddddddd |S: 0 4 2 6 1 5 3 7 |
D: dddddddd|S: 0 4 2 6 1 5 3 7|
This is the same, but blocked to 8 elements in the output. Unfortunately there is still a large spread of reads.
D:dddddddd |S:0 4 2 6 1 5 3 7 |
D: dddddddd |S: 0 4 2 6 1 5 3 7 |
D: dddddddd |S: 0 4 2 6 1 5 3 7 |
D: dddddddd|S: 0 4 2 6 1 5 3 7|
This is an attempt at improving the previous one - although the reads are still in a broad spread, they are always confined to 8 sequential streams. It does improve the performance once you get a large enough problem, but on an x86 machine N needs to be over about 8M before it shows a minor improvement. I've yet to try it on ARM.
Then I realised that Integer.reverse() wasn't mapping to a single instruction on x86 - and subsequently over half of the processing time was spent just calculating the source index ... so I put in a bit of bit-fiddling to the 8-blocked implementations which precalculated the 8 fixed element offsets relative to base-offset. I also tried a lookup table for the non-blocked implementation which made a big difference. Strangely using a lookup-table to get the base offset actually slowed it down - suggesting that the jvm is pre-calculating reverse(i) in the outer-loop if it can.
Once this permute is done the memory access pattern is just in adjacent and sequential blocks - either depth or breadth first. The 8-blocked permute is about 130%-150% of the speed of a straight System.arraycopy() for 4-1K elements.
Actually another reason I worked toward an 8-blocked implementation was in order to perform the first 8-way fft stage at the same time as the fiddling - with that in place I got to within shouting distance (under 200% execution time) of jtransforms for some small fft sizes. I was curious what I had to do to get better than that so I tried hard-coding the last stage of a size-16 fft and managed to beat it - not that this has any real practical purpose mind you.
This gives me a starting point to tackle the problem on the parallella which has it's own challenges.
PS yes I found a book or two and many papers about both fft implementation and the permute step but I had time to experiment on my own.
Java, C, SSE, poor mans lambdas
So after being able to avoid them for decades I got sucked in to having to do some matrix maths this week. I'm mostly just using a library but there were some memory and performance problems so I had to investigate my own matrix multiply routine.
Java vs gcc
Mostly just because of curiosity I tried comparing C to Java ... and the performance difference was negligble, actually sometimes the java cpu time is neglibly less. And i'm timing executing the programme from the command line - so that includes jvm startup and just-in-time compilation. I expected more of a difference in the obvious direction given the jvm overheads so that was a nice surprise. I suppose I shouldn't really be surprised by the performance anymore ...
And then further curiosity led me to attempting a vector based implementation - just using the gcc vector types. This was only about 2.4x faster - it would be worth it worth it, but I just used threads and it works fast enough anyway.
The vector implementation in gcc is simple, one just defines a vector type and then it's much the same as OpenCL, although one must ensure the data is aligned properly otherwise performance is pants.
TBH i'm a little dissapointed hotspot isn't doing any SSE optimisations here automatically (or maybe it is, but the execution time compared to C is too close for it to be a coincidence).
WorkPool
To implement the multi-threaded code I started using a poor-mans implementation of lambdas, or at least the parallel foreach part of it which is imho the main point of interest. I'm waiting for the jdk8 ga before pushing any java8 requirement onto my customer. It doesn't work as well as the lambda code in jdk8 but it isn't too far off and the syntax is fine as far as i'm concerned.
For simplicity I just have a static class which manages one thread per cpu with a simple static foreach call:
public class WorkPool {
... threads stuff ...
public interface WorkItem {
public void accept(int i);
}
public static synchronized void foreach(int start, int end, WorkItem job) {
... statically partition work across threads ...
... pass job to threads ...
... await completion ...
}
With obvious usage:
WorkPool.foreach(0, N, new WorkItem() {
public void accept(int i) {
array[i] = blah ...;
}
});
It's a bit clumsy without the 'effectively final' of Java8, and arguably clumsy due to the syntax but if each WorkItem does a sizable amount of work the overheads are acceptable. More importantly it just gets me thinking about how to solve problems in ways that will map immediately to Java8 when I start using it.
There's some other interesting stuff about the parallel execution model that I want to talk about but i'll leave that for another post. It's about mapping non-rectilinear work loads to a linear index and job execution order.
On another note, I keep running into problems with the thread job management on Java and keep end up having to write custom solutions. Executors seem like a great idea ... and they probably are for enterprise workloads but they basically suck for interactive desktop programmes - where you may be getting many many more update requests than you have time to process but you only need to keep (and must keep) the last one. Managing this with Future handles gets clumsy very fast. JavaFX comes with a new set of 'worker thread' primitives which I haven't really looked into much - they seemed to be light wrappers over existing functionality anyway and only seemed to muddy the waters last time I had a look.
One current implementation of WorkPool uses a ThreadPool executor but I will look at custom thread code too (curiosity again). Currently i'm also implementing static scheduling but it will be worth investigating something more dynamic.
fpu mode, compiler options
Poked a bit more at the 2d scaler on the parallella yesterday. I started just working out all the edge cases for the X scaler, but then I ended up delving into compiler options and assembler optimisations.
Because the floating point unit has some behaviour defined by the CONFIG register the compiler needs to twiddle bits quite a bit - and by default it seems to do it more often than you'd expect. And because it supports writing interrupt handlers in C it also requires any of these bit twiddles to occur within an interrupt disable block. Fun.
To cut a long story short I found that fiddling with the compiler flags makes a pretty big difference to performance.
The flags which seemed to produce the best result here were:
-std=gnu99 -O2 -ffast-math -mfp-mode=truncate -funroll-loops
Actually the option that has the biggest effect was -mfp-mode=truncate as that removes many of the (redundant) mode switches.
What I didn't expect though is that the CONFIG register bits also seem to have a big effect on the assembly code. By adding this to the preamble of the linear interpolator function I got a significant performance boost. Without it it's taking about 5.5Mcycles per core, but with it it's about 4.8Mcycles!?
mov r17,#0xfff0
movt r17,#0xfff1
mov r16,#1
movfs r12,CONFIG
and r12,r12,r17 ; set fpumode = float, turn off exceptions
orr r12,r12,r16 ; truncate rounding
movts CONFIG,r12
It didn't make any difference to the results whether I did this or not.
Not sure what's going on here.
I have a very simple routine that resamples a single line of float data using linear interpolation. I was trying to determine if such a simple routine would compile ok or would need me to resort to assembler language for decent performance. At first it looked like it was needed until I used the compiler flags above (although later I noticed I'd left an option to disable inlining of functions that I was using to investigate compiler output - which may have contributed).
The sampler i'm using is just (see: here for a nice overview):
static inline float sample_linear(float * __restrict__ src, float sxf) {
int sx = (int)sxf;
float r = sxf - sx;
float y1 = src[sx];
float y2 = src[sx+1];
return (y1*(1-r)+y2*r);
}
Called from:
static void scale_linex(float * __restrict__ src, float sxf, float * __restrict__ dst, int dlen, float factor) {
int x;
for (x=0;x<dlen;x++) {
dst[x] = sample(src, sxf);
sxf += factor;
}
}
A straight asm implementation is reasonably simple but there are a lot of dependency-stalls.
mov r19,#0 ; 1.0f
movt r19,#0x3f80
;; linear interpolation
fix r16,r1 ; sx = (int)sxf
lsl r18,r16,#2
float r17,r16 ; (float)sx
add r18,r18,r0
fsub r17,r1,r17 ; r = sxf - sx
ldr r21,[r18,#1] ; y2 = src[sx+1]
ldr r20,[r18,#0] ; y1 = src[sx]
fsub r22,r19,r17 ; 1-r
fmul r21,r21,r17 ; y2 = y2 * r
fmadd r21,r20,r22 ; res = y2 * r + y1 * (1-r)
(I actually implement the whole resample-row routine, not just the sampler).
This simple loop is much faster than the default -O2 optimisation, but slower than the C version with better optimisation flags. I can beat the C compiler with an implementation which processes 4 output pixels per loop - thus allowing for better scheduling with a reduction in stalls, and dword writes to the next core in the pipeline. But the gain is only modest for the amount of effort required.
Overview of
Routine Mcycles per core
C -O2 10.3
C flags as above 4.2
asm 1x 5.3
asm 1x force CONFIG 4.7
asm 4x 3.9
asm 4x force CONFIG 3.8
I'm timing the total instruction cycles on the core which includes the synchronisation work. Image is 512x512 scaled by 1.7x,1.0.
On a semi-relted note I was playing with the VJ detector code and noticed the performance scalability isn't quite so good on PAL-res images because in practice image being searched is very small. i.e. parallelism isn't so hot. I hit this problem with the OpenCL version too and probably the solution is the same as I used there: go wider. Basically generate all probe scales at once and then process them all at once.
Sharing DRAM on parallella - the easier way.
Currently parallella reserves a block of memory at a fixed physical address which the epiphany accesses directly and can be mapped to a linux process via e_alloc(). But as e_alloc() just calls mmap(NULL, ...) the linux-side address is different, and infact it will create a new alias for every e_alloc() invocation with the same parameters.
This makes it a bit of a pain to use as memory locations must be calculated manually via offsets on at least one end.
With the current parallella-16 the shared block is accessible on the epiphany via 0x8e000000, and I was wondering if that could just be mapped to the same location on the ARM side. It's been a while since I looked at the memory map of linux and i wasn't sure if there was anything there - and it turns out there isn't. Using cat /proc/pid/maps I found that it's somewhere between and a long way away from both the heap and the stack.
So ... if instead of calling e_alloc() you can just use mmap directly to create a shared area that can be used to pass complex linked data structures without having to perform any address remapping by hand - which is error prone and simply a big pita.
e.g. to map 8K at the start of this block on the parallella-16 I have:
// parallella-16: physical 3e000000 on arm == physical 8e000000 on epiphany
int fd = open("/dev/mem", O_RDWR | O_SYNC);
void *pmem = mmap((void *)0x8e000000, 8192, PROT_READ|PROT_WRITE, MAP_SHARED,
fd, 0x3e000000);
The specific numbers may vary on a given platform or configuration and can be determined at runtime.
This makes using the shared DRAM a lot easier including features like dynamic memory management (aka malloc).
Copyright (C) 2019 Michael Zucchi, All Rights Reserved.
Powered by gcc & me!